
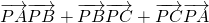 的最小值是
的最小值是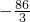
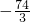
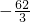
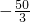
 、
、 、
、 的坐标关于x、y的坐标形式,从而算出
的坐标关于x、y的坐标形式,从而算出 、
、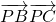 和
和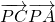 关于x、y的表达式,进而得到
关于x、y的表达式,进而得到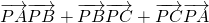 =3x2+3y2-10x-2y-12,再用配方法结合二次函数求最值的方法,即可算出所求的最小值.
=3x2+3y2-10x-2y-12,再用配方法结合二次函数求最值的方法,即可算出所求的最小值. =(1-x,4-y),
=(1-x,4-y), =(4-x,1-y),
=(4-x,1-y), =(-x,-4-y)
=(-x,-4-y) =(1-x)(4-x)+(4-y)(1-y)=x2+y2-5x-5y+8
=(1-x)(4-x)+(4-y)(1-y)=x2+y2-5x-5y+8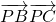 =(4-x)(-x)+(1-y)(-4-y)=x2+y2-4x+3y-4
=(4-x)(-x)+(1-y)(-4-y)=x2+y2-4x+3y-4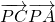 =(1-x)(-x)+(4-y)(-4-y)=x2+y2-x-16
=(1-x)(-x)+(4-y)(-4-y)=x2+y2-x-16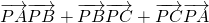 =3x2+3y2-10x-2y-12
=3x2+3y2-10x-2y-12 )2+3(y-
)2+3(y- )2
)2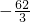
 且y=
且y= 时,
时,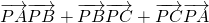 的最小值为
的最小值为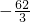


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com