
(本小题满分13分)对于定义域为D的函数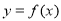 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[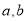 ]
] ,使
,使 在[
在[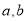 ]上的值域为[
]上的值域为[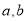 ];那么把
];那么把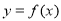 (
(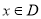 )叫闭函数。
)叫闭函数。
(1)求闭函数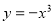 符合条件②的区间[
符合条件②的区间[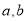 ];
];
(2)判断函数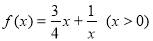 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(3)判断函数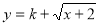 是否为闭函数?若是闭函数,求实数
是否为闭函数?若是闭函数,求实数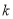 的取值范围。
的取值范围。
(1)[-1,1] (2)不是闭函数(3)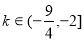
【解析】
试题分析:(Ⅰ)因为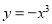 在R上单调递减,根据定义可知
在R上单调递减,根据定义可知 解方程就可以了.
解方程就可以了.
(Ⅱ)f(x)不是定义域内的单调函数,不满足闭函数的定义.
(Ⅲ) 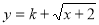 是单调递增函数,我们可以假设存在区间[a,b],使得
是单调递增函数,我们可以假设存在区间[a,b],使得 解方程
解方程
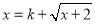 在定义域内有两不同的根.
在定义域内有两不同的根.
试题解析:(1)由题意,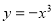 在[
在[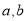 ]上递减,则
]上递减,则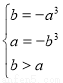 解得
解得
所以,所求的区间为[-1,1]
(2)取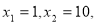 则
则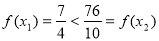 ,即
,即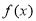 不是
不是 上的减函数。
上的减函数。
取
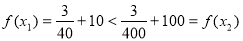 ,
,
即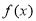 不是
不是 上的增函数
上的增函数
所以,函数在定义域内不单调递增或单调递减,从而该函数不是闭函数。
(3)若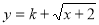 是闭函数,则存在区间[
是闭函数,则存在区间[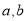 ],在区间[
],在区间[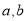 ]上,函数
]上,函数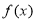 的值域为[
的值域为[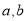 ],即
],即 ,
,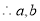 为方程
为方程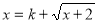 的两个实根,
的两个实根,
即方程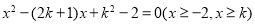 有两个不等的实根。
有两个不等的实根。
当 时,有
时,有 ,解得
,解得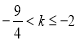 。当
。当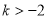 时,有
时,有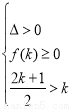 ,无解。
,无解。
综上所述,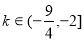 。
。
考点:新定义的应用,不等式


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源:2014-2015学年内蒙古巴彦淖尔市高一上学期期中考试数学试卷(解析版) 题型:选择题
若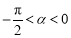 ,则点
,则点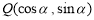 位于( )
位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省泰州市姜堰区高一上学期中考试数学试卷(解析版) 题型:填空题
设定义在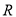 上的函数
上的函数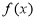 同时满足以下三个条件:①
同时满足以下三个条件:① 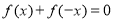 ;
;
② 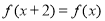 ;③当
;③当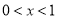 时,
时,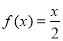 ,则
,则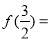 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省高一12月联考数学试卷(解析版) 题型:填空题
已知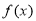 为
为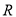 上的偶函数,对任意
上的偶函数,对任意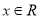 都有
都有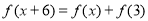 且当
且当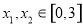 ,
,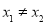 时,有
时,有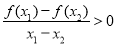 成立,给出四个命题:①
成立,给出四个命题:① ;②直线
;②直线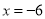 是函数
是函数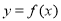 的图像的一条对称轴;③函数
的图像的一条对称轴;③函数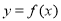 在
在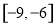 上为增函数;④函数
上为增函数;④函数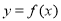 在
在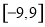 上有四个零点,其中所有正确命题的序号为 .
上有四个零点,其中所有正确命题的序号为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年湖南省高一12月联考数学试卷(解析版) 题型:选择题
用一个平面去截正方体,则截面不可能是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省等五校高三上学期第二次联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)已知数列 的各项均为正数,前
的各项均为正数,前 项和为
项和为 ,且
,且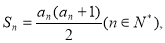
(Ⅰ)求证数列 是等差数列;
是等差数列;
(Ⅱ)设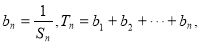 求
求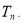
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com