
分析 (1)由题意设出椭圆方程,并得到b=1,结合椭圆的离心率及隐含条件列式求得a,则椭圆C的方程可求;
(2)设直线l的斜率为k,则直线l的方程是y=k(x-2).将直线l的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0.然后利用根与系数的关系证明λ1+λ2为定值.
解答 (1)解:由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$,
则2b=2,b=1,又$\frac{c}{a}=\frac{2\sqrt{5}}{5}$,可得$\frac{{c}^{2}}{{a}^{2}}=\frac{4}{5}$,
∵a2=b2+c2,∴可得a2=5.
∴椭圆C的方程为$\frac{{x}^{2}}{5}+{y}^{2}=1$;
(2)证明:设A、B、M点的坐标分别为A(x1,y1),B(x2,y2),M(0,y0).
又易知F点的坐标为(2,0).
显然直线l存在的斜率,设直线l的斜率为k,则直线l的方程是y=k(x-2).
将直线l的方程代入到椭圆C的方程中,消去y并整理得(1+5k2)x2-20k2x+20k2-5=0.
∴${x}_{1}+{x}_{2}=\frac{20{k}^{2}}{1+5{k}^{2}}$,${x}_{1}{x}_{2}=\frac{20{k}^{2}-5}{1+5{k}^{2}}$.
又∵$\overrightarrow{MA}={λ_1}\overrightarrow{AF},\overrightarrow{MB}={λ_2}\overrightarrow{BF}$,将各点坐标代入得${λ}_{1}=\frac{{x}_{1}}{2-{x}_{1}}$,${λ}_{2}=\frac{{x}_{2}}{2-{x}_{2}}$.
∴${λ}_{1}+{λ}_{2}=\frac{{x}_{1}}{2-{x}_{1}}+\frac{{x}_{2}}{2-{x}_{2}}$=$\frac{2({x}_{1}+{x}_{2})-2{x}_{1}{x}_{2}}{4-2({x}_{1}+{x}_{2})-{x}_{1}{x}_{2}}$=$\frac{2•\frac{20{k}^{2}}{1+5{k}^{2}}-2\frac{20{k}^{2}-5}{1+5{k}^{2}}}{4-2•\frac{20{k}^{2}}{1+5{k}^{2}}-\frac{20{k}^{2}-5}{1+5{k}^{2}}}$=-10.
点评 本题考查的知识点是椭圆的标准方程,直线与圆锥曲线的综合问题,其中根据已知条件计算出椭圆的标准方程是解答本题的关键,是中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:高中数学 来源: 题型:选择题
| A. | 4a-3 | B. | -1 | C. | 1 | D. | $\frac{5a-3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[-\sqrt{2},\sqrt{2}]$ | B. | $[1,\sqrt{2}]$ | C. | [2,3] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
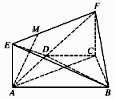 如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.
如图,在梯形ABCD中,AB∥CD,AD=CD=CB=a,∠ABC=60°,平面ACFE⊥平面ABCD,四边形ACFE是矩形,AE=a,点M在线段EF上,且MF=2EM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (¬p)∨q | B. | p∧q | C. | (¬p)∧(¬q) | D. | p∨(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
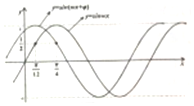
| A. | 沿x轴向左平移$\frac{π}{6}$个单位 | B. | 沿x轴向左平移$\frac{π}{3}$个单位 | ||
| C. | 沿x轴向右平移$\frac{π}{6}$个单位 | D. | 沿x轴向右平移$\frac{π}{6}$个单位 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com