
 CD,
CD,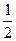 CD,CD=3,∴AH= AD=2.
CD,CD=3,∴AH= AD=2.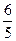 .
. 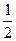 PA•AM=
PA•AM=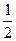 AN•PM,∴AN=
AN•PM,∴AN=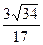 .
. 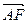 =(0,1,1),
=(0,1,1),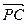 =(3,2,-2)
=(3,2,-2) 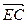 =(3-λ,2,0)
=(3-λ,2,0)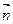 =(x,y,z),由
=(x,y,z),由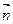 •
•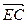 =0得(3-λ)x+2y=0,
=0得(3-λ)x+2y=0,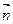 •
•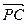 =0得3x+2y-2z=0,解得y=
=0得3x+2y-2z=0,解得y=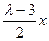 ,z=
,z= ;
;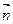 =(2,λ-3,λ)
=(2,λ-3,λ) 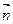 •
•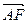 =0,即λ-3+λ=0,∴λ=
=0,即λ-3+λ=0,∴λ=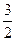
 =
=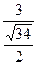 =
=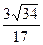


科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
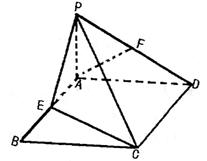
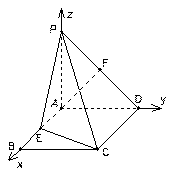
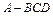 中,三条棱
中,三条棱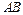 、
、 、
、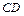 两两垂直,且
两两垂直,且 与平面
与平面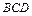 成
成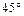 角,与平面
角,与平面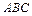 成
成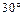 角.
角.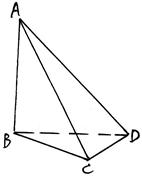
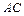 与平面
与平面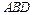 所成角的大小;
所成角的大小;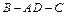 大小的余弦值.
大小的余弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
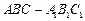 的底面是直角三角形,
的底面是直角三角形, ,侧棱与底面所成的角为
,侧棱与底面所成的角为 ,点
,点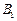 在底面上的射影
在底面上的射影 落在
落在 上.
上.
 恰为
恰为 的中点,且
的中点,且 ,求
,求 的值.
的值. ,且当
,且当 时,求二面角
时,求二面角 的大小.
的大小.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为
平方米的材料制成一个有盖的圆锥形容器,如果在制作过程中材料无损耗,且材料的厚度忽略不计,底面半径长为 ,圆锥母线的长为
,圆锥母线的长为

 与
与 的函数关系式,并写出
的函数关系式,并写出 的取值范围;(6分)
的取值范围;(6分) ,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)
,求所制作的圆锥形容器容积多少立方米(精确到0. 01m3) (6分)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com