已知在等差数列{an}中,a1=31,sn是它的前n项的和,s10=s22
(1)求sn;
(2)这个数列的前多少项的和最大,并求出这个最大值.
解:(1)∵s
10=a
1+a
2+…+a
10S
22=a
1+a
2+…+a
22,又s
10=S
22∴a
11+a
2+…+a
22=0
∴
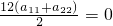
,即a
11+a
22=2a
1+31d=0,又a
1=31,
∴d=-2
∴
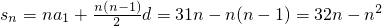
,
(2)∵s
n=32n-n
2∴当n=16时,s
n有最大值,s
n的最大值是256.
分析:(1)根据S
10=S
22,由等差数列的前n项和的公式可知,从第11项到第22项的和等于0,根据等差数列的前n项和的公式表示出第11项到第22项的和,然后利用等差数列的通项公式化简后得到首项和公差的关系式,把首项的值代入即可求出公差,利用首项和公差写出等差数列的前n项和的公式即可;
(2)根据(1)写出的前n项和的公式,发现S
n与n成的是二次函数关系,利用二次函数取最大值的方法即可求出S
n的最大值及此时n的值.
点评:此题考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值,掌握二次函数求最值的方法,是一道中档题.

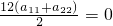 ,即a11+a22=2a1+31d=0,又a1=31,
,即a11+a22=2a1+31d=0,又a1=31,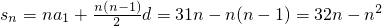 ,
,
