
【题目】椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() 为椭圆上一动点(异于左、右顶点),若
为椭圆上一动点(异于左、右顶点),若![]() 的周长为
的周长为![]() ,且面积的最大值为
,且面积的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是椭圆
是椭圆![]() 上两动点,线段
上两动点,线段![]() 的中点为
的中点为![]() ,
,![]() 的斜率分别为
的斜率分别为![]()
![]() 为坐标原点
为坐标原点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)通过2a+2c=![]() 且
且![]() ,计算即得结论;
,计算即得结论;
(2)当直线AB的斜率k=0时,|OP|![]() ,
,
当直线AB的斜率k≠0时,可令AB的方程为:x=my+t,由![]() 可得(m2+4)y2+2mty+t2﹣4=0,求得p(
可得(m2+4)y2+2mty+t2﹣4=0,求得p(![]() ,
,![]() ).由
).由![]() ,2t2=m2+4,代入|OP|2的运算中,化简得|OP|2
,2t2=m2+4,代入|OP|2的运算中,化简得|OP|2![]() ∈(
∈(![]() ,2]即可.
,2]即可.
(1)由题知,![]() 的周长为2a+2c=
的周长为2a+2c=![]() 且
且![]() ,
,
∴![]() ,c=
,c=![]()
∴椭圆C的方程为:![]() ;
;
(2)当直线AB的斜率k=0时,
此时k1,k2(O为坐标原点),满足![]() ,k1=-k2=﹣
,k1=-k2=﹣![]() .
.
可令OB的方程为:y![]() ,(xB>0)
,(xB>0)
由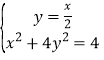 可得B(
可得B(![]() ,
,![]() ),
),
此时|OP|![]() ,
,
当直线AB的斜率k≠0时,可令AB的方程为:x=my+t,
由![]() 可得(m2+4)y2+2mty+t2﹣4=0,
可得(m2+4)y2+2mty+t2﹣4=0,
△=4m2t2﹣4(m2+4)(t2﹣4)>0m2﹣t2+4>0…①
![]() ,
,
x1+x2=m(y1+y2)+2t![]() .
.
∴p(![]() ,
,![]() ).
).
∵![]() ,∵
,∵![]() 4y1y2+x1x2=0.
4y1y2+x1x2=0.
(4+m2)y1y2+mt(y1+y2)+t2=0.
t2﹣4![]() t2=0.
t2=0.
2t2=m2+4,且t2≥2,…②
由①②可得t2≥2恒成立,
|OP|2![]() ∈(
∈(![]() ,2]
,2]
|OP|![]() .
.
综上,|OP|的取值范围为[![]() ,
,![]() ].
].


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】近日,某地普降暴雨,当地一大型提坝发生了渗水现象,当发现时已有![]() 的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为
的坝面渗水,经测算,坝而每平方米发生渗水现象的直接经济损失约为![]() 元,且渗水面积以每天
元,且渗水面积以每天![]() 的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积
的速度扩散.当地有关部门在发现的同时立即组织人员抢修渗水坝面,假定每位抢修人员平均每天可抢修渗水面积![]() ,该部门需支出服装补贴费为每人
,该部门需支出服装补贴费为每人![]() 元,劳务费及耗材费为每人每天
元,劳务费及耗材费为每人每天![]() 元.若安排
元.若安排![]() 名人员参与抢修,需要
名人员参与抢修,需要![]() 天完成抢修工作.
天完成抢修工作.
![]() 写出
写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
应安排多少名人员参与抢修,才能使总损失最小.(总损失=因渗水造成的直接损失+部门的各项支出费用)
查看答案和解析>>
科目:高中数学 来源: 题型:
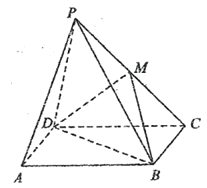
【题目】如图,在四棱锥P—ABCD中,四边形ABCD是矩形,平面PCD⊥平面ABCD,M为PC中点.求证:
(1)PA∥平面MDB;
(2)PD⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
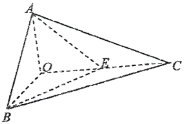
【题目】如图,已知三棱锥O—ABC的侧棱OA,OB,OC两两垂直,且OA=1,OB=OC=2,E是OC的中点.
(1)求异面直线BE与AC所成角的余弦值;
(2)求二面角A—BE—C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成5组:
年龄段的人员进行了调查研究,将各年龄段人数分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
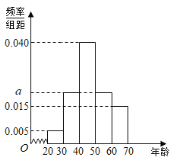
(1)求图中的a值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取8人,则三个组中,各抽取多少人;
(3)由频率分布直方图,求所有被调查人员的平均年龄.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】命题甲:“一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角相等或互补.”命题乙:“底面为正三角形,侧面为等腰三角形的三棱锥是正三棱锥.”命题丙:“过圆锥的两条母线的截面,以轴截面的面积最大.”其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com