
已知函数f(x)是定义在R上的偶函数,且x≥0时, .
.
(1)求f(-1)的值;
(2)求函数f(x)的值域A;
(3)设函数 的定义域为集合B,若AÍB,求实数a的取值范围.
的定义域为集合B,若AÍB,求实数a的取值范围.
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数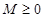 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.已知函数
的一个上界.已知函数 ,
, .
.
(1)若函数 为奇函数,求实数
为奇函数,求实数 的值;
的值;
(2)在(1)的条件下,求函数 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=2x- ,x∈(0,1].
,x∈(0,1].
(1)当a=-1时,求函数y=f(x)的值域;
(2)若函数y=f(x)在x∈(0,1]上是减函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知定义在R上的奇函数f(x)满足f(x-4)=-f(x).
(1)求f(2 012)的值;
(2)求证:函数f(x)的图像关于直线x=2对称;
(3)若f(x)在区间[0,2]上是增函数,试比较f(-25),f(11),f(80)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2+bx+c(b,c∈R),对任意的x∈R,恒有f′(x)≤f(x).
(1)证明:当x≥0时,f(x)≤(x+c)2;
(2)若对满足题设条件的任意b,c,不等式f(c)-f(b)≤M(c2-b2)恒成立,求M的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,
, .
.
(1)若 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若存在实数 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x3+ax-2,(a R).
R).
(l)若f(x)在区间(1,+ )上是增函数,求实数a的取值范围;
)上是增函数,求实数a的取值范围;
(2)若 ,且f(x0)=3,求x0的值;
,且f(x0)=3,求x0的值;
(3)若 ,且在R上是减函数,求实数a的取值范围。
,且在R上是减函数,求实数a的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com