
已知函数 ,
, .
.
(1)若 ,判断函数
,判断函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(2)若函数 在
在 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)若存在实数 使得关于
使得关于 的方程
的方程 有三个不相等的实数根,求实数
有三个不相等的实数根,求实数 的取值范围.
的取值范围.
(1)奇函数,(2) ,(3)
,(3) 
解析试题分析:(1)函数奇偶性的判定,一要判定定义域是否关于原点对称,二要判定 与
与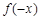 是否相等或相反,(2)函数
是否相等或相反,(2)函数 是分段函数,每一段都是二次函数的一部分,因此研究
是分段函数,每一段都是二次函数的一部分,因此研究 单调性,必须研究它们的对称轴,从图像可观察得到实数
单调性,必须研究它们的对称轴,从图像可观察得到实数 满足的条件:
满足的条件: ,(3)研究方程根的个数,通常从图像上研究,结合(2)可研究出函数
,(3)研究方程根的个数,通常从图像上研究,结合(2)可研究出函数 图像.分三种情况研究,一是
图像.分三种情况研究,一是 上单调增函数,二是先在
上单调增函数,二是先在 上单调增,后在
上单调增,后在 上单调减,再在
上单调减,再在 上单调增,三是先在
上单调增,三是先在 上单调增,后在
上单调增,后在 上单调减,再在
上单调减,再在 上单调增.
上单调增.
试题解析:(1)函数 为奇函数.[来
为奇函数.[来
当 时,
时, ,
, ,∴
,∴
∴函数 为奇函数; 3分
为奇函数; 3分
(2) ,当
,当 时,
时, 的对称轴为:
的对称轴为: ;
;
当 时,
时, 的对称轴为:
的对称轴为: ;∴当
;∴当 时,
时, 在R上是增函数,即
在R上是增函数,即 时,函数
时,函数 在
在 上是增函数; 7分
上是增函数; 7分
(3)方程 的解即为方程
的解即为方程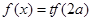 的解.
的解.
①当 时,函数
时,函数 在
在 上是增函数,∴关于
上是增函数,∴关于 的方程
的方程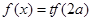 不可能有三个不相等的实数根; 9分
不可能有三个不相等的实数根; 9分
②当 时,即
时,即 ,∴
,∴ 在
在 上单调增,在
上单调增,在 上单调减,在
上单调减,在 上单调增,∴当
上单调增,∴当 时,关于
时,关于 的方程
的方程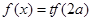 有三个不相等的实数根;即
有三个不相等的实数根;即 ,∵
,∵ ∴
∴ .
.
设 ,∵存在
,∵存在 使得关于
使得关于 的方程
的方程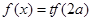 有三个不相等的实数根, ∴
有三个不相等的实数根, ∴ ,又可证
,又可证 在
在 上单调增
上单调增
∴ ∴
∴ ; 12分
; 12分
③当 时,即
时,即 ,∴
,∴


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)是定义在R上的偶函数,且x≥0时, .
.
(1)求f(-1)的值;
(2)求函数f(x)的值域A;
(3)设函数 的定义域为集合B,若AÍB,求实数a的取值范围.
的定义域为集合B,若AÍB,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 (
( ).
).
(1)证明:当 时,
时, 在
在 上是减函数,在
上是减函数,在 上是增函数,并写出当
上是增函数,并写出当 时
时 的单调区间;
的单调区间;
(2)已知函数 ,函数
,函数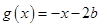 ,若对任意
,若对任意 ,总存在
,总存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数 ,如果满足:对任意
,如果满足:对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 是
是 上的有界函数,其中
上的有界函数,其中 称为函数
称为函数 的一个上界.
的一个上界.
已知函数 ,
, .
.
(1)若函数 为奇函数,求实数
为奇函数,求实数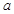 的值;
的值;
(2)在(1)的条件下,求函数 在区间
在区间 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数 在
在 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数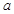 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设定义域为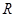 的函数
的函数
(Ⅰ)在平面直角坐标系内作出函数 的图象,并指出
的图象,并指出 的单调区间(不需证明);
的单调区间(不需证明);
(Ⅱ)若方程 有两个解,求出
有两个解,求出 的取值范围(只需简单说明,不需严格证明).
的取值范围(只需简单说明,不需严格证明).
(Ⅲ)设定义为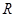 的函数
的函数 为奇函数,且当
为奇函数,且当 时,
时, 求
求 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com