
【题目】如图,在四棱锥P﹣ABCD中,AD∥BC,AB⊥AD,E是AB的中点,AB=AD=PA=PB=2,BC=1,PC= ![]() .
. 
(1)求证:CF∥平面PAB;
(2)求证:PE⊥平面ABCD;
(3)求二面角B﹣PA﹣C的余弦值.
【答案】
(1)证明:取AP的中点M,连接MF,MB,
因为M是AP中点,F是PD中点,
所以 ![]() ,
,
又因为 ![]() ,
,
所以四边形BCFM是平行四边形,所以FC∥BM,
又FC面ABP,BM面ABP
所以FC∥面ABP
(2)证明:连接CE,
因为在△ABP中,AB=AP=BP,点E是边AB在的中点,
所以PE⊥AB且 ![]() ,
,
在Rt△BEC中,BE=EC=1,EB⊥BC,所以 ![]()
在△PEC中, ![]() ,
, ![]() ,
, ![]() ,
,
所以PE⊥EC
又因为AB∩EC=E,AB面ABCD,EC面ABCD
所以PE⊥面ABCD
(3)解:取CD中点N,以EB,EN,EP分别为轴x,y轴,z轴,建立空间直角坐标系,各点坐标为:B(1,0,0),C(1,1,0),B(1,0,0), ![]() ,A(﹣1,0,0),
,A(﹣1,0,0),
因为:BC⊥PE,AB⊥BC,所以BC⊥面ABP,面ABP的法向量为 ![]()
设面ABP的法向量为 ![]()
![]() ,
, ![]() ,
,
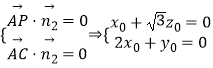 ,取x0=1,得
,取x0=1,得 ![]() ,
,
由图可知二面角为锐二面角,设锐二面角为θ,
![]() ,
,
二面角B﹣PA﹣C余弦值为 ![]() .
.
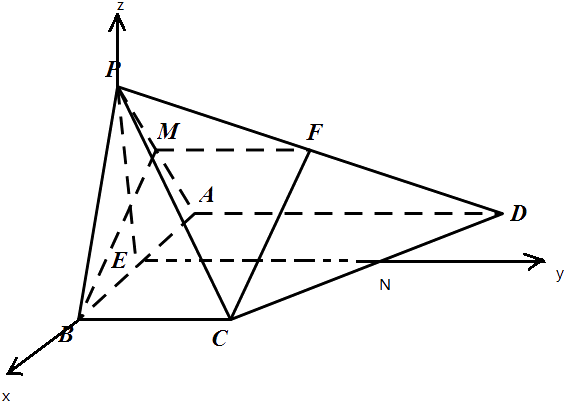
【解析】(1)取AP的中点M,连接MF,MB,推导出四边形BCFM是平行四边形,从而FC∥BM,由此能证明FC∥面ABP.(2)连接CE,推导出PE⊥AB,PE⊥EC,由此能证明PE⊥面ABCD.(3)取CD中点N,以EB,EN,EP分别为轴x,y轴,z轴,建立空间直角坐标系,利用向量法能求出二面角B﹣PA﹣C余弦值.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定和直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且满足ccosB=(2a+b)cos(π﹣C).
(1)求角C的大小;
(2)若c=4,△ABC的面积为 ![]() ,求a+b的值.
,求a+b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项等差数列{an}的前n项和为Sn , 且满足 ![]() ,S7=56.
,S7=56.
(1)求数列{an}的通项公式an;
(2)若数列{bn}满足b1=a1且bn+1﹣bn=an+1 , 求数列 ![]() 的前n项和Tn .
的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的顶点与焦点分别是椭圆![]() 的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定点M(1,0)和直线x=﹣1上的动点N(﹣1,t),线段MN的垂直平分线交直线y=t于点R,设点R的轨迹为曲线E.
(1)求曲线E的方程;
(2)直线y=kx+b(k≠0)交x轴于点C,交曲线E于不同的两点A,B,点B关于x轴的对称点为点P.点C关于y轴的对称点为Q,求证:A,P,Q三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}(n=1,2,3,…)满足an+1=2an , 且a1 , a2+1,a3成等差数列,设bn=3log2an﹣7.
(1)求数列{an},{bn}的通项公式;
(2)求数列{|bn|}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体A-BCD中,AD![]() 平面BCD,BC
平面BCD,BC![]() CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
CD,CD=2,AD=4.M是AD的中点,P是BM的中点,点Q在线段AC上,且AQ=3QC.
(I)证明:PQ//平面BCD;
(II)若异面直线PQ与CD所成的角为![]() ,二面角C-BM-D的大小为
,二面角C-BM-D的大小为![]() ,求cos
,求cos![]() 的值。
的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com