
分析 (1)依题意列关于m的不等式组,求解不等式组得答案;
(2)当m=4时,求出圆C1的方程,得到圆心坐标和半径,进一步求出关于x+y=0对称的圆C2方程,得到C2(-2,-1).
(i)要存在无穷多对直线L1与L2,必有无穷多对的斜率都存在,设L1的斜率为k,P(m,n),则L2的斜率为$-\frac{1}{k}$,求出L1,L2的方程,由两圆半径都等于1,因此,若相交弦长相等,则两圆心到对应直线的距离必相等,列式可得(m-n-2)k-(m+n)=0或(m+n)k+(m-n+4)=0对无穷多个k值成立.由此求得m值,得到
点P的坐标;
(ii)设C1到MN的距离为d,则PM•PN=$(\sqrt{P{{C}_{1}}^{2}-{d}^{2}}-\sqrt{1-{d}^{2}})(\sqrt{P{{C}_{1}}^{2}-{d}^{2}}-\sqrt{1-{d}^{2}})=P{{C}_{1}}^{2}-1=8$,同理PR•PS,代入${S_1}•{S_2}=\frac{1}{4}PM•PR•PN•PS=16$
得S1•S2为定值16.
解答 解:(1)依题意$\left\{\begin{array}{l}2-2-4+m>0\\ 4+16-4m>0\end{array}\right.$,解得4<m<5;
(2)当m=4时,C1:(x-1)2+(y-2)2=1是以C1(1,2)为圆心,半径为1的圆,
∴它关于x+y=0对称的圆C2方程为(x+2)2+(y+1)2=1,C2(-2,-1).
(i)∵要存在无穷多对直线L1与L2,∴必有无穷多对的斜率都存在,
设L1的斜率为k,P(m,n),则L2的斜率为$-\frac{1}{k}$,
∴L1:kx-y-mk+n=0,L2:x+ky-m-kn=0,
由于两圆半径都等于1,因此,若相交弦长相等,则两圆心到对应直线的距离必相等,
∴$\frac{|k-2-mk+n|}{{\sqrt{{k^2}+1}}}$=$\frac{|-2-k-m-kn|}{{\sqrt{{k^2}-1}}}?|(m-1)k-(n-2)|=|k(n+1)+(m+2)|$
?(m-1)k-(n-2)=k(n+1)+(m+2)或(m-1)k-(n-2)=-k(n+1)-(m+2),
即(m-n-2)k-(m+n)=0或(m+n)k+(m-n+4)=0对无穷多个k值成立.
∴$\left\{\begin{array}{l}m-n-2=0\\ m=-n\end{array}\right.$或$\left\{\begin{array}{l}m-n+4=0\\ m=-n\end{array}\right.$,
解得$\left\{\begin{array}{l}m=1\\ m=-1\end{array}\right.$或$\left\{\begin{array}{l}m=-2\\ m=2\end{array}\right.$,
∴点P的坐标为(1,-1)或(-2,2);
(ii)设C1到MN的距离为d,则PM•PN=$(\sqrt{P{{C}_{1}}^{2}-{d}^{2}}-\sqrt{1-{d}^{2}})(\sqrt{P{{C}_{1}}^{2}-{d}^{2}}-\sqrt{1-{d}^{2}})=P{{C}_{1}}^{2}-1=8$,
同理,PR•PS=$(\sqrt{P{{C}_{2}}^{2}-{d}^{2}}-\sqrt{1-{d}^{2}})(\sqrt{P{{C}_{2}}^{2}-{d}^{2}}-\sqrt{1-{d}^{2}})=P{{C}_{2}}^{2}-1=8$,
又${S_1}•{S_2}=\frac{1}{4}PM•PR•PN•PS=16$,
∴S1•S2为定值16.
点评 本题考查圆的方程,考查了直线与圆位置关系的应用,考查数学转化思想方法,训练了计算能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
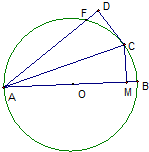 如图所示,AB是⊙O的直径,点C在⊙O上,CD为⊙O的切线,过A作CD的垂线,垂足为D,交⊙O于F.
如图所示,AB是⊙O的直径,点C在⊙O上,CD为⊙O的切线,过A作CD的垂线,垂足为D,交⊙O于F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连结OD交圆O于点M.且AB=4,DE=$\frac{3}{2}$.
如图所示,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,点D是BC边的中点,连结OD交圆O于点M.且AB=4,DE=$\frac{3}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AB=BC=2,AD=CD=$\sqrt{7}$,PA=$\sqrt{3}$,∠ABC=120°,G为线段PC上的点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 30 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0,005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com