
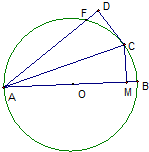
 如图所示,AB是⊙O的直径,点C在⊙O上,CD为⊙O的切线,过A作CD的垂线,垂足为D,交⊙O于F.
如图所示,AB是⊙O的直径,点C在⊙O上,CD为⊙O的切线,过A作CD的垂线,垂足为D,交⊙O于F.分析 (1)连接OC,运用圆的切线的性质和两直线平行的判定和性质,由内角平分线的定义,即可得证;
(2)由AC⊥BC,CM为斜边AB上的高,运用直角三角形的射影定理,结合圆的切割线定理,即可得到所求值.
解答 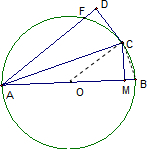 解:(1)证明:连接OC,
解:(1)证明:连接OC,
CD为⊙O的切线,可得OC⊥CD,
又AD⊥CD,
可得OC∥AD,
所以∠CAD=∠ACO,
又OC=OA,所以∠CAO=∠ACO,
所以∠CAO=∠CAD
所以AC为∠DAB的角平分线.
(2)由题意⊙O的直径为8,OM:MB=3:1,
可得OM=3,MB=1,
由AC⊥BC,CM为斜边AB上的高,
可得CM2=AM•MB=7,
又AC=AC,∠CAO=∠CAD,
所以Rt△ACB≌Rt△ACD,
所以CD=CM,
又CD2=DF•DA,
而CD2=7.
所以DF•DA=7.
点评 本题考查圆的切线的性质和直角三角形的射影定理、切割线定理的运用,考查三角形全等和内角平分线的定义,考查推理和运算能力,属于中档题.


 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在△ABC中,∠BAC的平分线交BC于D,交△ABC的外接圆于E,延长AC交△DCE的外接圆于F
如图,在△ABC中,∠BAC的平分线交BC于D,交△ABC的外接圆于E,延长AC交△DCE的外接圆于F查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在圆内接四边形ABCD中,AD为圆的直径,对角线AC与BD交于点Q,AB,DC的延长线交于点P,连接PQ并延长交AD于点E,连接EB.
在圆内接四边形ABCD中,AD为圆的直径,对角线AC与BD交于点Q,AB,DC的延长线交于点P,连接PQ并延长交AD于点E,连接EB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
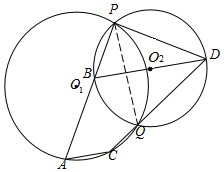 如图,☉O1,☉O2交于两点P,Q,直线AB过点P,与⊙O1,⊙O2分别交于点A,B,直线CD过点Q,与⊙O1,⊙O2分别交于点C,D.求证:AC∥BD.
如图,☉O1,☉O2交于两点P,Q,直线AB过点P,与⊙O1,⊙O2分别交于点A,B,直线CD过点Q,与⊙O1,⊙O2分别交于点C,D.求证:AC∥BD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com