
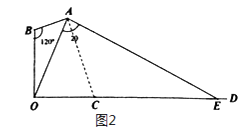
【题目】如图1,在路边安装路灯,路宽为OD,灯柱OB长为h米,灯杆AB长为1米,且灯杆与灯柱成120°角,路灯采用圆锥形灯罩,其轴截面的顶角为2θ,灯罩轴线AC与灯杆AB垂直. 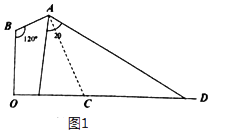
(1)设灯罩轴线与路面的交点为C,若OC=5 ![]() 米,求灯柱OB长;
米,求灯柱OB长;
(2)设h=10米,若灯罩轴截面的两条母线所在直线一条恰好经过点O,另一条与地面的交点为E(如图2); 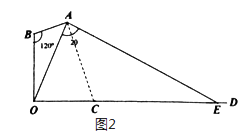
(i)求cosθ的值;
(ii)求该路灯照在路面上的宽度OE的长;
【答案】
(1)解:过A作AE⊥OD,垂足为E,过B作BF⊥AE,垂足为F,
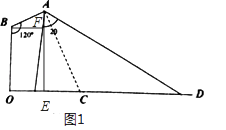
则∠ABF=120°﹣90°=30°,
∴AF= ![]() AB=
AB= ![]() ,BF=
,BF= ![]() AB=
AB= ![]() ,
,
∴OE=BF= ![]() ,
,
∴CE=OC﹣OE= ![]() .
.
在四边形ABOC中,∵∠BOC=∠BAC=90°,∠ABO=120°,
∴∠ACO=60°,
在Rt△ACE中,tan∠ACE= ![]() =
= ![]() ,
,
∴AE= ![]() CE=
CE= ![]() ,
,
∴OB=EF=AE﹣AF=13.
即灯柱OB高13米.
(2)解:(i)在△ABO中,由余弦定理得OA= ![]() =
= ![]() ,
,
由正弦定理得 ![]() =
= ![]() ,∴sin∠BAO=
,∴sin∠BAO= 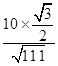 =
= ![]() .
.
∴cosθ=sin∠BAO= ![]() .
.
(ii)sinθ= ![]() =
= ![]() ,sin2θ=2sinθcosθ=
,sin2θ=2sinθcosθ= ![]() ,
,
∴sin∠AEO=sin(60°﹣θ)= ![]() ﹣
﹣ ![]() =
= ![]() .
.
在△AOE中,由正弦定理得 ![]() =
= ![]() ,
,
解得OE= ![]() =
= ![]() .
.
【解析】(1)作AE⊥OD,BF⊥AE,求出AF,BF,得出CE的长,根据tan∠ACE= ![]() 求出AE,从而得出OB的长;(2)(i)在△AOB中,利用正弦定理求出sin∠BAO即可得出cosθ;(ii)利用差角公式计算sin∠AEO,在△AOE中,利用正弦定理计算OE.
求出AE,从而得出OB的长;(2)(i)在△AOB中,利用正弦定理求出sin∠BAO即可得出cosθ;(ii)利用差角公式计算sin∠AEO,在△AOE中,利用正弦定理计算OE.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,BC=2AC,分别以A、B为圆心,AC的长为半径作扇形ACD和扇形BEF,D、E在AB上,F在BC上.在△ACB中任取一点,这一点恰好在图中阴影部分的概率是( ) 
A.![]()
B.1﹣ ![]()
C.![]()
D.1﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知(a2+b2)sin(A﹣B)=(a2﹣b2)sin(A+B),则△ABC的形状( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙M:(x+1)2+y2= ![]() 的圆心为M,⊙N:(x﹣1)2+y2=
的圆心为M,⊙N:(x﹣1)2+y2= ![]() 的圆心为N,一动圆M内切,与圆N外切. (Ⅰ)求动圆圆心P的轨迹方程;
的圆心为N,一动圆M内切,与圆N外切. (Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)设A,B分别为曲线P与x轴的左右两个交点,过点(1,0)的直线l与曲线P交于C,D两点.若 ![]() =12,求直线l的方程.
=12,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)同时满足①f(x)为偶函数;②对任意x,有f( ![]() ﹣x)=f(
﹣x)=f( ![]() +x),则函数f(x)的解析式可以是( )
+x),则函数f(x)的解析式可以是( )
A.f(x)=cos2x
B.![]()
C.f(x)=cos6x
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知: ![]() 、
、 ![]() 、
、 ![]() 是同一平面上的三个向量,其中
是同一平面上的三个向量,其中 ![]() =(1,2).
=(1,2).
(1)若| ![]() |=2
|=2 ![]() ,且
,且 ![]() ∥
∥ ![]() ,求
,求 ![]() 的坐标.
的坐标.
(2)若| ![]() |=
|= ![]() ,且
,且 ![]() +2
+2 ![]() 与2
与2 ![]() ﹣
﹣ ![]() 垂直,求
垂直,求 ![]() 与
与 ![]() 的夹角θ
的夹角θ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 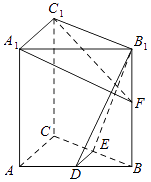
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com