
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 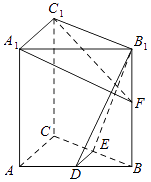
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
【答案】
(1)证明:∵D,E为中点,
∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC﹣A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1平面A1C1F,且DEA1C1F,
∴DE∥平面A1C1F
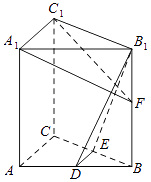
(2)证明:∵ABC﹣A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D平面B1DE,
∴A1F⊥平面B1DE,
又∵A1FA1C1F,∴平面B1DE⊥平面A1C1F
【解析】(1)推导出DE∥AC,从而DE∥A1C1 , 由此能证明DE∥平面A1C1F.(2)推导出AA1⊥A1C1 , 从而A1C1⊥平面AA1B1B,进而DE⊥平面AA1B1B,再由DE⊥A1F,得A1F⊥平面B1DE,由此能证明平面B1DE⊥平面A1C1F.


科目:高中数学 来源: 题型:
【题目】如图1,在路边安装路灯,路宽为OD,灯柱OB长为h米,灯杆AB长为1米,且灯杆与灯柱成120°角,路灯采用圆锥形灯罩,其轴截面的顶角为2θ,灯罩轴线AC与灯杆AB垂直. 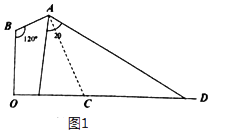
(1)设灯罩轴线与路面的交点为C,若OC=5 ![]() 米,求灯柱OB长;
米,求灯柱OB长;
(2)设h=10米,若灯罩轴截面的两条母线所在直线一条恰好经过点O,另一条与地面的交点为E(如图2); 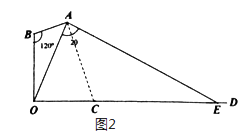
(i)求cosθ的值;
(ii)求该路灯照在路面上的宽度OE的长;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为1的正项数列{an}满足an+12+an2< ![]() ,n∈N* , Sn为数列{an}的前n项和.
,n∈N* , Sn为数列{an}的前n项和.
(1)若a2= ![]() ,a3=x,a4=4,求x的取值范围;
,a3=x,a4=4,求x的取值范围;
(2)设数列{an}是公比为q的等比数列,若 ![]() <Sn+1<2Sn , n∈N* , 求q的取值范围;
<Sn+1<2Sn , n∈N* , 求q的取值范围;
(3)若a1 , a2 , …,ak(k≥3)成等差数列,且a1+a2+…+ak=120,求正整数k的最小值,以及k取最小值时相应数列a1 , a2 , …,ak .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn , 且an= ![]() (n∈N*). (Ⅰ)若数列{an+t}是等比数列,求t的值;
(n∈N*). (Ⅰ)若数列{an+t}是等比数列,求t的值;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)记bn= ![]() +
+ ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知ω>0,0<φ<π,直线x= ![]() 和x=
和x= ![]() 是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则
是函数f(x)=sin(ωx+φ)图象的两条相邻的对称轴,则
(1)求f(x)的解析式;
(2)设h(x)=f(x)+ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求分别满足下列条件的直线l的方程:
(1)斜率是 ![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0)、B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com