
【题目】城市公交车的数量若太多则容易造成资源的浪费;若太少又难以满足乘客需求.某市公交公司在某站台的60名候车乘客中随机抽取15人,将他们的候车时间作为样本分成5组,如下表所示(单位:分钟):
组别 | 候车时间 | 人数 |
一 |
| 2 |
二 |
| 6 |
三 |
| 4 |
四 |
| 2 |
五 |
| 1 |
(1)估计这60名乘客中候车时间少于10分钟的人数;
(2)若从上表第三、四组的6人中任选2人作进一步的调查,求抽到的两人恰好来自不同组的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)用候车时间少于![]() 分钟的总人数除以
分钟的总人数除以![]() ,得到的频率再乘以
,得到的频率再乘以![]() ,即可得到结果;(2)先计算从三、四两组中任选2人的基本事件个数,为此,将第三组乘客编号为
,即可得到结果;(2)先计算从三、四两组中任选2人的基本事件个数,为此,将第三组乘客编号为![]() ,第四组乘客编号为
,第四组乘客编号为![]() ,列出基本事件的空间,利用古典概型的概率公式,即可求解概率.
,列出基本事件的空间,利用古典概型的概率公式,即可求解概率.
试题解析:(1)用候车时间少于10分钟的总人数除以15,得到的频率再乘以60;
(2)先计算从三、四两组中任选2人的基本事件个数,为此,将第三组乘客编号为![]() ,第四组乘客编号为
,第四组乘客编号为![]() ,选中
,选中![]() 的事件有
的事件有![]() 共5个,未选中
共5个,未选中![]() 而选中
而选中![]() 的事件有
的事件有![]() 共4个,
共4个,![]() 都未选中而选中
都未选中而选中![]() 的事件有
的事件有![]() 共3个,
共3个, ![]() 都未选中而选中
都未选中而选中![]() 的事件有
的事件有![]() 共2个,选中的两人都来自四组的事件为
共2个,选中的两人都来自四组的事件为![]() 共1个,所以共15个基本事件,其中2人恰好来自不同组的事件有
共1个,所以共15个基本事件,其中2人恰好来自不同组的事件有![]() 共8个,
共8个,
后者除以前者即得![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】(多选)某小组有三名男生和两名女生,从中任选两名去参加比赛,则下列各对事件中为互斥事件的是( )
A.恰有一名男生和全是男生B.至少有一名男生和至少有一名女生
C.至少有一名男生和全是男生D.至少有一名男生和全是女生
查看答案和解析>>
科目:高中数学 来源: 题型:
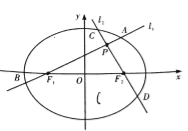
【题目】如图,分别过椭圆![]() 左、右焦点
左、右焦点![]() 的动直线
的动直线![]() 相交于
相交于![]() 点,与椭圆
点,与椭圆![]() 分别交于
分别交于![]() 与
与![]() 不同四点,直线
不同四点,直线![]() 的斜率
的斜率![]() 满足
满足![]() , 已知
, 已知![]() 与
与![]() 轴重合时,
轴重合时, ![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在定点![]() 使得
使得![]() 为定值,若存在,求出
为定值,若存在,求出![]() 点坐标并求出此定值,若不存在,
点坐标并求出此定值,若不存在,
说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(2)当![]() 时,判断
时,判断![]() 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数![]() 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数![]() ,都存在以
,都存在以![]() 为边长的三角形.
为边长的三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为![]() ,通过
,通过![]() 块玻璃以后强度为
块玻璃以后强度为![]() .
.
(Ⅰ)写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅱ)通过多少块玻璃以后,光线强度减弱到原来的![]() 以下.(lg3≈0.4771).
以下.(lg3≈0.4771).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场有奖销售中,购满100元商品得1张奖券,多购多得,1000张奖券为一个开奖单位,设特等奖1个,一等奖10个,二等奖50个.设1张奖券中特等奖、一等奖、二等奖的事件分别为A、B、C,求:
(1)P(A),P(B),P(C);
(2)1张奖券的中奖概率;
(3)1张奖券不中特等奖且不中一等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com