己知数列
是各项均为正数的等差数列，其中
，且
，
，
构成等比数列：数列
的前
项和为
，满足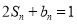
．
（1）求数列，的通项公式；
（2）如果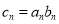
，设数列
的前
项和为
，是否存在正整数
，使得
成立，若存在，求出
的最小值，若不存在，说明理由．
科目：高中数学 来源：2015-2016学年河北省高二下期中文科数学试卷（解析版） 题型：解答题
按照某学者的理论，假设一个人生产某产品单件成本为
元，如果他卖出该产品的单价为
元，则他的满意度为
；如果他买进该产品的单价为
元，则他的满意度为
．如果一个人对两种交易（卖出或买进）的满意度分别为
和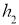
，则他对这两种交易的综合满意度为
．
现假设甲生产A、B两种产品的单件成本分别为12元和5元，乙生产A、B两种产品的单件成本分别为3元和20元，设产品A、B的单价分别为
元和
元，甲买进A与卖出B的综合满意度为
，乙卖出A与买进B的综合满意度为
（1）求和关于、的表达式；当
时，求证：=；
（2）设，当、分别为多少时，甲、乙两人的综合满意度均最大？最大的综合满意度为多少？
查看答案和解析>>
科目：高中数学 来源：2015-2016学年河北省高二下期中理科数学试卷（解析版） 题型：选择题
已知随机变量X服从正态分布N（μ，σ2），且P（μ－2σ＜X＜μ＋2σ）＝0.954 4，P（μ－σ＜X＜μ＋σ）＝0.682 6.若μ＝4，σ＝1，则P（5＜X＜6）＝（ ）
A．0.135 9 B．0.135 8 C．0.271 8 D．0.271 6；
查看答案和解析>>
科目：高中数学 来源：2017届江西省、宜春一中高三7月联考文科数学试卷（解析版） 题型：选择题
函数
的最小正周期是
，若其图象向右平移
个单位后得到的函数为奇函数，则函数
的图象（ ）
A．关于点
对称
B．关于直线
对称
C．关于点
对称
D．关于直线
对称
查看答案和解析>>
科目：高中数学 来源：2017届广州省惠州市高三第一次调研文科数学试卷（解析版） 题型：解答题
已知函数
的部分图像如图所示.
（Ⅰ）求函数
的解析式，并写出
的单调减区间；
（Ⅱ）已知
的内角分别是
，
为锐角，且
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
在R上是奇函数，且满足
，当
时，
，则
（ ）
，那么
（ ）
在
处与直线
相切，则
．
展开式的常数项为15，则
______．