
【题目】已知 ![]() 中,
中, ![]() 分别为两腰上的高、求证:
分别为两腰上的高、求证: ![]()
【答案】【解答】
证明:如图,以 BC 所在直线为 x 轴, BC 的垂直平分线为 y 轴建立平面直角坐标系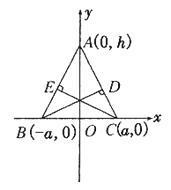
设 ![]()
则直线 AC 的方程为 ,![]()
即: ![]()
直线 AB 的方程为 ,![]()
即: ![]()
由点到直线的距离公式: ,![]()
![]()
∴ ![]() ,即 BD=CE
,即 BD=CE
【解析】本题考查坐标法在几何中的应用、解答本题可通过建立平面直角坐标系,将几何证明问题转化为代数运算问题(1)建立适当的直角坐标系,将平面几何问题转化为解析几何问题,即“形”转化为“数”,再回到“形”中,此为坐标法的基本思想,务必熟练掌握(2)建立坐标系时,要充分利用图形的几何特征、例如,中心对称图形,可利用它的对称中心为坐标原点;轴对称图形,可利用它的对称轴为坐标轴;设中有直角,可考虑以两直角边所在的直线为坐标轴等。


科目:高中数学 来源: 题型:
【题目】已知下列三个命题:
①若一个球的半径缩小到原来的 ![]() ,则其体积缩小到原来的
,则其体积缩小到原来的![]() ;
;
②若两组数据的平均数相等,则它们的标准差也相等;
③直线x+y+1=0与圆x2+y2= ![]() 相切.
相切.
其中真命题的序号是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知指数函数y=g(x)满足:g(3)=8,定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(1)确定y=f(x)和y=g(x)的解析式;
(2)若对任意的x∈[1,4],不等式f(2x﹣3)+f(x﹣k)>0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为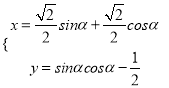 (
(![]() 为参数),若以直角坐标系中的原点为极点,
为参数),若以直角坐标系中的原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() 为实数.)
为实数.)
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与曲线
与曲线![]() 有公共点,求
有公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系: f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(Ⅰ)求实验室这一天的最大温差;
(Ⅱ)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在极坐标系中,圆![]() 的极坐标方程为:
的极坐标方程为: ![]() .若以极点
.若以极点![]() 为原点,极轴所在直线为
为原点,极轴所在直线为![]() 轴建立平面直角坐标系.
轴建立平面直角坐标系.
(Ⅰ)求圆![]() 的直角坐标方程及其参数方程;
的直角坐标方程及其参数方程;
(Ⅱ)在直角坐标系中,点![]() 是圆
是圆![]() 上动点,求
上动点,求![]() 的最大值,并求出此时
的最大值,并求出此时
点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)= ![]() +alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
+alnx﹣3x,g(x)=﹣x2+8x,且x=1是函数f(x)的极大值点.
(1)求a的值.
(2)如果函数y=f(x)和函数y=g(x)在区间(b,b+1)上均为增函数,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察高中生的性别与是否喜欢数学课程之间的关系,在我市某普通中学高中生中随机抽取200名学生,得到如下2×2列联表:
喜欢数学课 | 不喜欢数学课 | 合计 | |
男 | 30 | 60 | 90 |
女 | 20 | 90 | 110 |
合计 | 50 | 150 | 200 |
经计算K2≈6.06,根据独立性检验的基本思想,约有(填百分数)的把握认为“性别与喜欢数学课之间有关系”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com