
已知a为常数,函数f(x)=x(lnx-ax)有两个极值点x1,x2(x1<x2),则( )
A.f(x1)>0,f(x2)>- B.f(x1)<0,f(x2)<-
B.f(x1)<0,f(x2)<-
C.f(x1)>0,f(x2)<- D.f(x1)<0,f(x2)>-
D.f(x1)<0,f(x2)>-
D
[解析] 由题意知,函数f(x)=x(lnx-ax)=xlnx-ax2有两个极值点,
即f ′(x)=lnx+1-2ax=0在区间(0,+∞)上有两个根.
令h(x)=lnx+1-2ax,则h′(x)=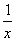 -2a=
-2a=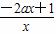 ,当a≤0时h′(x)>0,h(x)在区间(0,+∞)上递增,f ′(x)=0不可能有两个正根,
,当a≤0时h′(x)>0,h(x)在区间(0,+∞)上递增,f ′(x)=0不可能有两个正根,
∴a>0.由h′(x)=0,可得x=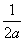 ,从而可知h(x)在区间(0,
,从而可知h(x)在区间(0,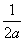 )上递增,在区间(
)上递增,在区间(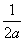 ,+∞)上递减.因此需h(
,+∞)上递减.因此需h(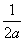 )=ln
)=ln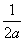 +1-1=ln
+1-1=ln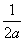 >0,即
>0,即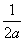 >1时满足条件,故当0<a<
>1时满足条件,故当0<a< 时,h(x)=0有两个根x1,x2,且x1<
时,h(x)=0有两个根x1,x2,且x1<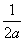 <x2.
<x2.
又h(1)=1-2a>0,∴x1<1<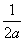 <x2,从而可知函数f(x)在区间(0,x1)上递减,在区间(x1,x2)上递增,在区间(x2,+∞)上递减.
<x2,从而可知函数f(x)在区间(0,x1)上递减,在区间(x1,x2)上递增,在区间(x2,+∞)上递减.
∴f(x1)<f(1)=-a<0,f(x2)>f(1)=-a>- .故选D.
.故选D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
设函数f(x)在R上可导,其导函数为f ′(x),且函数y=(1-x)f ′(x)的图象如下图所示,则下列结论中一定成立的是( )
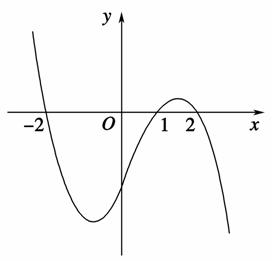
A.函数f(x)有极大值f(2)和极小值f(1)
B.函数f(x)有极大值f(-2)和极小值f(1)
C.函数f(x)有极大值f(2)和极小值f(-2)
D.函数f(x)有极大值f(-2)和极小值f(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a、b的值;
(2)求函数f(x)的单调区间与极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
设D是函数y=f(x)定义域内的一个区间,若存在x0∈D,使f(x0)=-x0,则称x0是f(x)的一个“次不动点”.若函数f(x)=ax2-3x-a+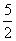 在区间[1,4]上存在次不动点,则实数a的取值范围是( )
在区间[1,4]上存在次不动点,则实数a的取值范围是( )
A.(-∞,0) B.(0, )
)
C.[ ,+∞) D.(-∞,
,+∞) D.(-∞, ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
对于三次函数y=ax3+bx2+cx+d(a≠0),给出定义:设f ′(x)是函数y=f(x)的导数,f ″(x)是f ′(x)的导数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.若f(x)=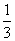 x3-
x3-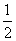 x2+3x-
x2+3x-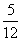 ,根据这一发现可得:
,根据这一发现可得:
(1)函数f(x)=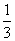 x3-
x3-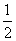 x2+3x-
x2+3x-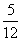 的对称中心为________;
的对称中心为________;
(2)计算f(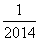 )+f(
)+f(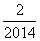 )+f(
)+f(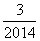 )+f(
)+f(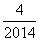 )+…+f(
)+…+f(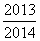 )=________.
)=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com