在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系．已知点A的极坐标为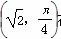
，直线l的极坐标方程为ρcos
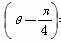＝a，且点A在直线l上．
(1)求a的值及直线l的直角坐标方程；
(2)圆C的参数方程为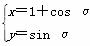
(α为参数)，试判断直线l与圆C的位置关系．
备战中考寒假系列答案科目：高中数学 来源： 题型：
如图,在半径为
、圆心角为60°的扇形的
弧上任取一点
,作扇形的内接矩形
,使点
在
上,点
在
上,设矩形的面积为
.
(1) 按下列要求写出函数关系式：
① 设
,将表示成
的函数关系式；
② 设
,将表示成
的函数关系式.
(2) 请你选用(Ⅰ)中的一个函数关系式,求的最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
为迎接6月6日的“全国爱眼日”，某高中学校学生会随机抽取16名学生，经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎，小数点后的一位数字为叶)如图，若视力测试结果不低于5.0，则称为“好视力”．
(1)写出这组数据的众数和中位数；
(2)求从这16人中随机选取3人，至少有2人是“好视力”的概率；
(3)以这16人的样本数据来估计整个学校的总体数据，若从该校(人数很多)任选3人，记X表示抽到“好视力”学生的人数，求X的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
在平面直角坐标系中，已知直线l：ρcos θ＋ρsin θ＝2(θ为参数)和曲线C：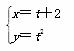
(t为参数)，若l与C相交于A、B两点，则|AB|＝________.
查看答案和解析>>
科目：高中数学 来源： 题型：
在平面直角坐标系xOy中，直线l的参数方程为
(t为参数)，P、Q分别为直线l与x轴、y轴的交点，线段PQ的中点为M.
(1)求直线l的直角坐标方程；
(2)以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标和直线OM的极坐标方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
马老师从课本上抄录一个随机变量ξ的概率分布列如下表：
| x | 1 | 2 | 3 |
| P(ξ＝x) | ？ | ！ | ？ |
请小牛同学计算ξ的数学期望．尽管“！”处完全无法看清，且两个“？”处字迹模糊，但能断定这两个“？”处的数值相同，据此，小牛给出了正确答案E(ξ)＝________.
查看答案和解析>>
科目：高中数学 来源： 题型：
某学校为响应省政府号召，每学期派老师到各个民工子弟学校支教，以下是该学校50名老师上学期在某一个民工子弟学校支教的次数统计结果：
| 支教次数 | 0 | 1 | 2 | 3 |
| 人数 | 5 | 10 | 20 | 15 |
根据上表信息解答以下问题：
(1)从该学校任选两名老师，用η表示这两人支教次数之和，记“函数f(x)＝x2－ηx－1在区间(4,5)上有且只有一个零点”为事件A，求事件A发生的概率P1；
(2)从该学校任选两名老师，用ξ表示这两人支教次数之差的绝对值，求随机变量ξ的分布列及数学期望E(ξ)．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.
＝
<1，所以直线l与圆C相交．
，则函数
的最小值为 .
的焦点到准线的距离是（ ）
D．