在平面直角坐标系xOy中，直线l的参数方程为
(t为参数)，P、Q分别为直线l与x轴、y轴的交点，线段PQ的中点为M.
(1)求直线l的直角坐标方程；
(2)以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标和直线OM的极坐标方程．
名师指导期末冲刺卷系列答案科目：高中数学 来源： 题型：
在平面直角坐标系中，以坐标原点为极点，x轴的非负半轴为极轴建立极坐标系．已知点A的极坐标为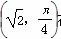
，直线l的极坐标方程为ρcos
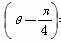＝a，且点A在直线l上．
(1)求a的值及直线l的直角坐标方程；
(2)圆C的参数方程为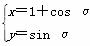
(α为参数)，试判断直线l与圆C的位置关系．
查看答案和解析>>
科目：高中数学 来源： 题型：
设10≤x1<x2<x3<x4≤104，x5＝105.随机变量ξ1取值x1，x2，x3，x4，x5的概率均为0.2，随机变量ξ2取值
的概率也均为0.2.若记Dξ1，Dξ2分别为ξ1，ξ2的方差，则( )
A．D(ξ1)>D(ξ2)
B．D(ξ1)＝D(ξ2)
C．D(ξ1)<D(ξ2)
D．D(ξ1)与D(ξ2)的大小关系与x1，x2，x3，x4的取值有关
查看答案和解析>>
科目：高中数学 来源： 题型：
某数学兴趣小组共10名学生，参加一次只有5道填空题的测试．填空第i题的难度计算公式为Pi＝
(其中Ri为答对该题的人数，N为参加测试的总人数)．该次测试每道填空题的考前预估难度P
及考后实测难度Pi的数据如下表：
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度P | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 考后实测难度Pi | 0.8 | 0.8 | 0.7 | 0.7 | 0.2 |
(1)定义描述填空题难度预估值与实测值偏离程度的统计量为
S＝
[(P
－P1)2＋(P
－P2)2＋…＋(P
－Pn)2]．若S<0.01，则称填空题的难度预估是合理的，否则为不合理．请你判断该次测试填空题的难度预估是否合理？并说明理由．
(2)从该小组中随机抽取2名学生，记被抽取的学生中第5题答对的人数为ξ，求ξ的分布列及数学期望．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知直线
和双曲线
相交于A，B两点，线段AB的中点为M.设直线的斜率为k1(k1≠0)，直线OM的斜率为k2,则k1k2=（ ）
A. 
B. - C. -
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
得
x＋y－2
＝2和tan θ＝
＝
，
(ρ∈R).
，则△ABC的面积为（ ）
B． 
C．
D．.
的图象经过点
，
，当
时，恒有
，求实数
的取值范围.
(α为参数)与曲线ρ2－2ρcos θ＝0的交点个数为________．
的焦点到准线的距离是（ ）
D．