
分析 建立直角坐标系,设出点的坐标,线段BC的中点,AC的中点,由$\overrightarrow{BC}$⊥$\overrightarrow{PM}$,$\overrightarrow{AC}$⊥$\overrightarrow{QM}$,可得结论.
解答 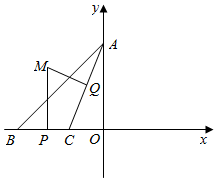 解:(1)建立如图所示的直角坐标系
解:(1)建立如图所示的直角坐标系
设A(0,3),B(x0-2,0),C(x0+2,0),外心M(x,y)
则线段BC的中点P(x0,0),AC的中点Q($\frac{{x}_{0}+2}{2}$,$\frac{3}{2}$)
∴$\overrightarrow{BC}$=(4,0),$\overrightarrow{AC}$=(x0+2,-3),$\overrightarrow{PM}$=(x-x0,y),
$\overrightarrow{QM}$=(x-$\frac{{x}_{0}+2}{2}$,y-$\frac{3}{2}$),
由$\overrightarrow{BC}$⊥$\overrightarrow{PM}$,$\overrightarrow{AC}$⊥$\overrightarrow{QM}$,可得$\left\{\begin{array}{l}{4(x-{x}_{0})=0}\\{({x}_{0}+2)(x-\frac{{x}_{0}+2}{2})+(-3)(y-\frac{3}{2})=0}\end{array}\right.$
消去x0可得:x2=6y-5.
点评 本题考查轨迹方程,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 已知直线l:y=-x+1与椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为($\frac{2}{3}$,$\frac{1}{3}$)
已知直线l:y=-x+1与椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0))相交于不同的两点A、B,且线段AB的中点P的坐标为($\frac{2}{3}$,$\frac{1}{3}$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 合格品数 | 次品数 | 总数 | |
| 第一台加工数 | 45 | 10 | 55 |
| 第二台加工数 | 40 | 5 | 45 |
| 总计 | 85 | 15 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15种 | B. | 30种 | C. | 90种 | D. | 180种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
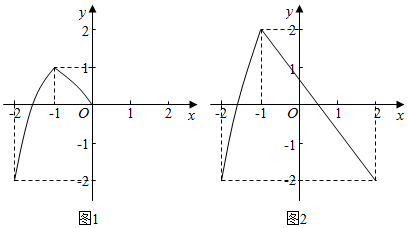
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com