
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж14ЗжЃЉЃЉ
ФГЪпВЫЛљЕижжжВЮїКьЪСЃЌгЩРњФъЪаГЁааЧщЕУжЊЃЌДгЖўдТвЛШеЦ№ЕФ300ЬьФкЃЌЮїКьЪСГЁЪлМлгыЩЯЪаЪБМфЕФЙиЯЕгУЭМвЛЕФвЛЬѕелЯпБэЪОЃЛЮїКьЪСЕФжжжВГЩБОгыЩЯЪаЪБМфЕФЙиЯЕгУЭМЖўЕФХзЮяЯпЖЮБэЪОЁЃ
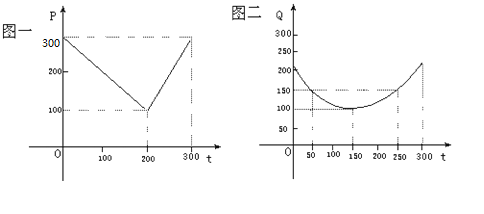
ЃЈЂёЃЉаДГіЭМвЛБэЪОЕФЪаГЁЪлМлгыЪБМфЕФКЏЪ§ЙиЯЕЪН![]() ЃЛаДГіЭМЖўБэЪОЕФжжжВГЩБОгыЩЯЪаЪБМфЕФКЏЪ§ЙиЯЕЪН
ЃЛаДГіЭМЖўБэЪОЕФжжжВГЩБОгыЩЯЪаЪБМфЕФКЏЪ§ЙиЯЕЪН![]() ЃЛ
ЃЛ
ЃЈЂђЃЉМйШчЩшЖЈЪаГЁЪлМлМѕШЅжжжВГЩБОЮЊДПЪевцЃЌЮЪКЮЪБЩЯЪаЕФЮїКьЪСДПЪевцзюДѓЃПЃЈзЂЃКЪаГЁЪлМлКЭжжжВГЩБОЕФЕЅЮЛЃКдЊ/102ЉKЃЌЪБМфЕЅЮЛЃКЬьЃЉ
ЁОД№АИЁПЃЈ1ЃЉ![]()
![]()
ЃЈ2ЃЉДгЖўдТвЛШеПЊЪМЕФЕк50ЬьЪБЃЌЩЯЪаЕФЮїКьЪСДПЪевцзюДѓ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКБОЬтЪЧКЏЪ§гІгУЬтЃЌЃЈ1ЃЉКЏЪ§ЙиЯЕЪНаЮЪНЬтжавбОИјГіЃЌ![]() ЪЧЗжЙРКЏЪ§ЃЌЭМЯѓЪЧСНЖЮЯпЖЮЃЌвЛДЮКЏЪ§ЕФаЮЪНЃЌЗжБ№ЧѓГіМДПЩЃЌ
ЪЧЗжЙРКЏЪ§ЃЌЭМЯѓЪЧСНЖЮЯпЖЮЃЌвЛДЮКЏЪ§ЕФаЮЪНЃЌЗжБ№ЧѓГіМДПЩЃЌ![]() ЪЧХзЮяЯпЃЌЖўДЮКЏЪ§ЃЌНтЮіЪНПЩЩшЮЊвЛАуЪНЛђЖЅЕуЪНЃЛЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУДПЪевц
ЪЧХзЮяЯпЃЌЖўДЮКЏЪ§ЃЌНтЮіЪНПЩЩшЮЊвЛАуЪНЛђЖЅЕуЪНЃЛЃЈ2ЃЉгЩЃЈ1ЃЉПЩЕУДПЪевц![]() ЃЌШдЪЧЗжЖЮКЏЪ§ЃЌЦфзюДѓжЕвЊЗжЖЮЧѓГіЃЌдйШЁзюДѓЕФвЛИіЃЎ
ЃЌШдЪЧЗжЖЮКЏЪ§ЃЌЦфзюДѓжЕвЊЗжЖЮЧѓГіЃЌдйШЁзюДѓЕФвЛИіЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЭМ1ПЩЕУЪаГЁЪлМлгыЪБМфЕФКЏЪ§ЙиЯЕЮЊ![]()
гЩЭМ2ПЩЕУжжжВГЩБОгыЪБМфЕФКЏЪ§ЙиЯЕЮЊ![]()

ЃЈ2ЃЉЩш![]() ЪБПЬЕФДПЪевцЮЊ
ЪБПЬЕФДПЪевцЮЊ![]() ЃЌдђгЩЬтвтЕУ
ЃЌдђгЩЬтвтЕУ![]() ЃЌ
ЃЌ
МД
ЕБ![]() ЪБЃЌХфЗНећРэЃЌЕУ
ЪБЃЌХфЗНећРэЃЌЕУ![]()
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУЧјМф
ШЁЕУЧјМф![]() ЩЯЕФзюДѓжЕ100ЃЛ
ЩЯЕФзюДѓжЕ100ЃЛ
ЕБ![]() ЪБЃЌХфЗНећРэЃЌЕУ
ЪБЃЌХфЗНећРэЃЌЕУ![]()
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУЧјМф
ШЁЕУЧјМф![]() ЩЯЕФзюДѓжЕ87ЃЎ5ЃЛ
ЩЯЕФзюДѓжЕ87ЃЎ5ЃЛ
злЩЯПЩжЊ![]() дкЧјМф
дкЧјМф![]() ЩЯПЩвдШЁЕНзюДѓжЕ100ЃЌДЫЪБЃЌ
ЩЯПЩвдШЁЕНзюДѓжЕ100ЃЌДЫЪБЃЌ![]() ЃЌМДДгЖўдТвЛШеПЊЪМЕФЕк50ЬьЪБЃЌЩЯЪаЕФЮїКьЪСЪевцзюДѓ100ЁЃ
ЃЌМДДгЖўдТвЛШеПЊЪМЕФЕк50ЬьЪБЃЌЩЯЪаЕФЮїКьЪСЪевцзюДѓ100ЁЃ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕШВюЪ§Са{an}ЕФЙЋВюdЁй0ЃЌЫќЕФЧАnЯюКЭЮЊSnЃЌШєS5ЃН70ЃЌЧвa2ЃЌa7ЃЌa22ГЩЕШБШЪ§СаЃЎ
(1)ЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
(2)ЩшЪ§Са![]() ЕФЧАnЯюКЭЮЊTnЃЌЧѓжЄЃК
ЕФЧАnЯюКЭЮЊTnЃЌЧѓжЄЃК ![]() ЁмTnЃМ
ЁмTnЃМ![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИідВзЖЕФЕзУцАыОЖЮЊ2ЃЌИпЮЊ6ЃЌдкЦфжагавЛИіИпЮЊxЕФФкНгдВжљЃЎ
(1)гУxБэЪОдВжљЕФжсНиУцУцЛ§SЃЛ
(2)ЕБxЮЊКЮжЕЪБЃЌSзюДѓЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊУќЬт![]() ЁАДцдк
ЁАДцдк![]() ЁБЃЌУќЬт
ЁБЃЌУќЬт![]() ЃКЁАЧњЯп
ЃКЁАЧњЯп![]() БэЪОНЙЕудк
БэЪОНЙЕудк![]() жсЩЯЕФЭждВЁБЃЌУќЬт
жсЩЯЕФЭждВЁБЃЌУќЬт![]() ЁАЧњЯп
ЁАЧњЯп![]() БэЪОЫЋЧњЯпЁБ
БэЪОЫЋЧњЯпЁБ
ЃЈ1ЃЉШєЁА![]() Чв
Чв![]() ЁБЪЧецУќЬтЃЌЧѓЪЕЪ§
ЁБЪЧецУќЬтЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉШє![]() ЪЧ
ЪЧ![]() ЕФБивЊВЛГфЗжЬѕМўЃЌЧѓЪЕЪ§
ЕФБивЊВЛГфЗжЬѕМўЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
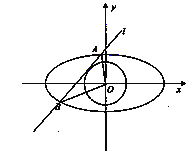
ЁОЬтФПЁПШчЭМ,жБЯп![]() гыдВO:
гыдВO: ![]() ЧвгыЭждВC:
ЧвгыЭждВC: ![]() ЯрНЛгкA,BСНЕу
ЯрНЛгкA,BСНЕу
(1)ШєжБЯп![]() ЧЁКУОЙ§ЭждВЕФзѓЖЅЕу,ЧѓЯвГЄAB;
ЧЁКУОЙ§ЭждВЕФзѓЖЅЕу,ЧѓЯвГЄAB;
(2)ЩшжБЯпOA,OBЕФаБТЪЗжБ№ЮЊk1,k2,ХаЖЯk1ЁЄk2ЪЧЗёЮЊЖЈжЕ,ВЂЫЕУїРэгЩ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
ЃЈ1ЃЉЧѓКЏЪ§![]() ЕФзюаЁе§жмЦкгыЕЅЕїЕнМѕЧјМфЃЛ
ЕФзюаЁе§жмЦкгыЕЅЕїЕнМѕЧјМфЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() ЕФЭМЯѓЩЯЕФЫљгаЕуЕФКсзјБъЩьГЄЕНдРДЕФ
ЕФЭМЯѓЩЯЕФЫљгаЕуЕФКсзјБъЩьГЄЕНдРДЕФ![]() БЖЃЌЫљЕУЕФЭМЯѓгыжБЯп
БЖЃЌЫљЕУЕФЭМЯѓгыжБЯп![]() НЛЕуЕФКсзјБъгЩаЁЕНДѓвРДЮЪЧ
НЛЕуЕФКсзјБъгЩаЁЕНДѓвРДЮЪЧ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ14ЗжЃЉЙигкxЕФВЛЕШЪНax2+ЃЈaЉ2ЃЉxЉ2Ён0ЃЈaЁЪRЃЉ
ЃЈ1ЃЉвбжЊВЛЕШЪНЕФНтМЏЮЊЃЈЉЁоЃЌЉ1]ЁШ[2ЃЌ+ЁоЃЉЃЌЧѓaЕФжЕЃЛ
ЃЈ2ЃЉНтЙигкxЕФВЛЕШЪНax2+ЃЈaЉ2ЃЉxЉ2Ён0ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊШ§РтзЖSЉABCЕФИїЖЅЕуЖМдквЛИіАыОЖЮЊrЕФЧђУцЩЯЃЌЧвSA=SB=SC=1ЃЌAB=BC=AC=![]() ЃЌдђЧђЕФБэУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЌдђЧђЕФБэУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A. 12Іа B. 8Іа C. 4Іа D. 3Іа
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшЪ§Са{an}ЕФЧАnЯюКЭЮЊSnЃН2n2ЃЌ{bn}ЮЊЕШБШЪ§СаЃЌЧвa1ЃНb1ЃЌb2(a2Ѓa1)ЃНb1ЃЎ
(1)ЧѓЪ§Са{an}КЭ{bn}ЕФЭЈЯюЙЋЪНЃЛ
(2)ЩшcnЃН![]() ЃЌЧѓЪ§Са{cn}ЕФЧАnЯюКЭTnЃЎ
ЃЌЧѓЪ§Са{cn}ЕФЧАnЯюКЭTnЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com