练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知三棱锥S﹣ABC的各顶点都在一个半径为r的球面上，且SA=SB=SC=1，AB=BC=AC=，则球的表面积为（　　）

    A. 12π B. 8π C. 4π D. 3π

    【答案】D

    【解析】试题分析：由题意一个三棱锥S﹣ABC的三条侧棱SA、SB、SC两两互相垂直，可知，三棱锥是正方体的一个角，扩展为正方体，两者的外接球相同，正方体的对角线就是球的直径，求出直径即可求出球的表面积．

    详解：三棱锥S﹣ABC中，SA=SB=SC=1，AB=BC=AC=，

    ∴共顶点S的三条棱两两相互垂直，且其长均为1，

    三棱锥的四个顶点同在一个球面上，三棱锥是正方体的一个角，扩展为正方体，

    三棱锥的外接球与正方体的外接球相同，正方体的对角线就是球的直径，

    所以球的直径为：，半径为，

    外接球的表面积为：4π×（）2=3π．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知双曲线过点(3,-2)且与椭圆4x2+9y2=36有相同的焦点.

    (I)求双曲线的标准方程.

    (II)若点M在双曲线上, 是双曲线的左、右焦点,且|MF1|+|MF2|=试判断的形状.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分14分））

    某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿场售价与上市时间的关系用图一的一条折线表示；西红柿的种植成本与上市时间的关系用图二的抛物线段表示。

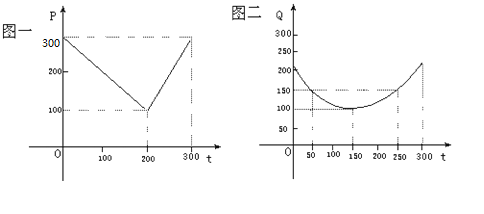
    （Ⅰ）写出图一表示的市场售价与时间的函数关系式；写出图二表示的种植成本与上市时间的函数关系式；

    （Ⅱ）假如设定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？（注：市场售价和种植成本的单位：元/102㎏，时间单位：天）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列{an}满足：a1=，a2=，且a1a2+a2a3+…+anan+1=na1an+1对任何的正整数n都成立，则的值为（　　）

    A. 5032 B. 5044 C. 5048 D. 5050

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设x，y满足约束条件 ，若目标函数2z=2x+ny（n＞0），z的最大值为2，则y=tan（nx+ ）的图象向右平移 后的表达式为（ ）
    A.y=tan（2x+ ）
    B.y=tan（x﹣ ）
    C.y=tan（2x﹣ ）
    D.y=tan2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}的前n项和是Sn，且Sn=1（n∈N），数列{bn}是公差d不等于0的等差数列，且满足：b1=，而b2，b5，ba14成等比数列．

    （1）求数列{an}、{bn}的通项公式；

    （2）设cn=anbn，求数列{cn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， ， ， ， .

    （1）在平面内找一点，使得直线平面，并说明理由；

    （2）证明：平面平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为矩形， 平面， ， 为中点．

    （I）证明： 平面．

    （II）证明： 平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，已知多面体中，四边形为矩形， ， ，平面平面， 、分别为、的中点．

    （）求证： ．

    （）求证： 平面．

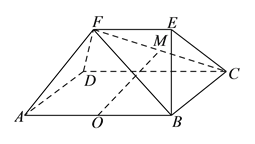
    （）若过的平面交于点，交于，求证： ．

    查看答案和解析>>

    同步练习册答案