
【题目】已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=﹣2.
(1)判断f(x)的奇偶性及单调性并证明你的结论;
(2)若对任意x∈R,不等式f(ax2)﹣2f(x)<f(x)+4恒成立,求a的取值范围.
【答案】
(1)解:取x=y=0,则f(0+0)=2f(0),∴f(0)=0.
取y=﹣x,则f(x﹣x)=f(x)+f(﹣x),
∴f(﹣x)=﹣f(x)对任意x∈R恒成立,∴f(x)为奇函数.
任取x1,x2∈(﹣∞,+∞),且x1<x2,则x2﹣x1>0,f(x2)+f(﹣x1)=f(x2﹣x1)<0,
∴f(x2)<﹣f(﹣x1),又f(x)为奇函数,
∴f(x1)>f(x2).
∴f(x)是R上的减函数
(2)解:f(x)为奇函数,整理原式得f(ax2)+f(﹣2x)<f(x)+f(﹣2),
则f(ax2﹣2x)<f(x﹣2),
∵f(x)在(﹣∞,+∞)上是减函数,∴ax2﹣2x>x﹣2,
当a=0时,﹣2x>x﹣2在R上不是恒成立,与题意矛盾;
当a>0时,ax2﹣2x﹣x+2>0,要使不等式恒成立,则△=9﹣8a<0,即a> ![]() ;
;
当a<0时,ax2﹣3x+2>0在R上不是恒成立,不合题意.
综上所述,a的取值范围为( ![]() ,+∞)
,+∞)
【解析】(1)取x=y=0,则f(0+0)=2f(0),可得f(0)=0.取y=﹣x,则f(x﹣x)=f(x)+f(﹣x),即可判断出奇偶性.任取x1 , x2∈(﹣∞,+∞),且x1<x2 , 可得x2﹣x1>0,f(x2)+f(﹣x1)=f(x2﹣x1)<0,化简即可得出单调性.(2)利用函数的奇偶性与单调性、不等式的解法即可得出.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
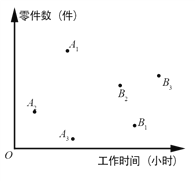
【题目】三名工人加工同一种零件,他们在一天中的工作情况如图所示,其中点Ai的横、纵坐标分别为第i名工人上午的工作时间和加工的学科&网零件数,点Bi的横、纵坐标分别为第i名工人下午的工作时间和加工的零件数,i=1,2,3.
①记Qi为第i名工人在这一天中加工的零件总数,则Q1,Q2,Q3中最大的是_________.
②记pi为第i名工人在这一天中平均每小时加工的零件数,则p1,p2,p3中最大的是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面几何中有如下结论:正三角形ABC的内切圆面积为S1 , 外接圆面积为S2 , 则 ![]() ,推广到空间可以得到类似结论;已知正四面体P﹣ABC的内切球体积为V1 , 外接球体积为V2 , 则
,推广到空间可以得到类似结论;已知正四面体P﹣ABC的内切球体积为V1 , 外接球体积为V2 , 则 ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P是圆x2+y2=4上一动点,PD⊥x轴于点D,记满足 ![]() =
= ![]() (
( ![]() +
+ ![]() )的动点M的轨迹为Γ. (Ⅰ)求轨迹Γ的方程;
)的动点M的轨迹为Γ. (Ⅰ)求轨迹Γ的方程;
(Ⅱ)已知直线l:y=kx+m与轨迹F交于不同两点A,B,点G是线段AB中点,射线OG交轨迹Γ于点Q,且 ![]() =λ
=λ ![]() ,λ∈R.
,λ∈R.
①证明:λ2m2=4k2+1;
②求△AOB的面积S(λ)的解析式,并计算S(λ)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,已知acosB+bcosA=2ccosC.
(1)求角C的大小;
(2)若a=5,b=8,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=a(x-lnx)+![]() ,a∈R.
,a∈R.
(I)讨论f(x)的单调性;
(II)当a=1时,证明f(x)>f’(x)+![]() 对于任意的x∈[1,2] 恒成立。
对于任意的x∈[1,2] 恒成立。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax3+bx2+2x在x=﹣1处取得极值,且在点(1,f(1))处的切线的斜率为2. (Ⅰ)求a,b的值:
(Ⅱ)若关于x的方程f(x)+x3﹣2x2﹣x+m=0在[ ![]() ,2]上恰有两个不相等的实数根,求实数m的取值范围.
,2]上恰有两个不相等的实数根,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两家商场对同一种商品展开促销活动,对购买该商品的顾客两家商场的奖励方案如下:
甲商场:顾客转动如图所示转盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为![]() ,边界忽略不计)即为中奖.
,边界忽略不计)即为中奖.
乙商场:从装有4个白球,4个红球和4个篮球的盒子中一次性摸出3球(这些球初颜色外完全相同),如果摸到的是3个不同颜色的球,即为中奖.

(Ⅰ)试问:购买该商品的顾客在哪家商场中奖的可能性大?说明理由;
(Ⅱ)记在乙商场购买该商品的顾客摸到篮球的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com