
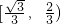
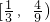
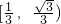
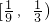
 =
=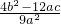 =
=
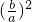 +
+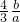 +
+ ,由f′0)•f′(1)>0,
,由f′0)•f′(1)>0, <-1,利用二次函数的性质求出
<-1,利用二次函数的性质求出 的范围,即可求得|x1-x2|的取值范围.
的范围,即可求得|x1-x2|的取值范围.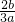 ,x1•x2=
,x1•x2=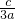 .∴|x1-x2|2 =
.∴|x1-x2|2 =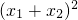 -4x1x2 ,
-4x1x2 , =
=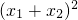 -4x1•x2 =
-4x1•x2 =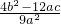 .
. =
=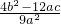 =
=
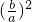 +
+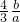 +
+ .
.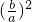 +3
+3  +2<0,解得-2<
+2<0,解得-2< <-1.
<-1. =-
=- 时,
时, 有最小值为
有最小值为  ,
, 趋于-1时,
趋于-1时, 趋于
趋于  ,故
,故  ∈
∈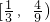 ,
,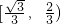 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| π | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | -0.61 | -0.59 | -0.56 | -0.35 | 0 | 0.26 | 0.42 | 1.57 | 3.27 |
| y | 0.07 | 0.02 | -0.03 | -0.22 | 0 | 0.21 | 0.20 | -10.04 | -101.63 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com