
分析 设2x=t(1≤t≤2),即有g(t)=at-t2,求出对称轴方程,讨论区间[1,2]和对称轴的关系,运用单调性可得最大值.
解答 解:设2x=t(1≤t≤2),
即有g(t)=at-t2,
对称轴为t=$\frac{a}{2}$,
当$\frac{a}{2}$≥2时,即a≥4,区间[1,2]递增,
可得t=2即x=1时,取得最大值2a-4;
当1<$\frac{a}{2}$<2时,即2<a<4时,t=$\frac{a}{2}$时,即x=log2$\frac{a}{2}$,取得最大值$\frac{{a}^{2}}{4}$;
当$\frac{a}{2}$≤1时,即a≤2,区间[1,2]递减,
可得t=1即x=0时,取得最大值a-1.
综上可得,a≤2时,f(x)的最大值为a-1;
2<a<4时,f(x)的最大值为$\frac{{a}^{2}}{4}$;
a≥4时,f(x)的最大值为2a-4.
点评 本题考查可化为二次函数的最值的求法,注意讨论对称轴和区间的关系,考查运算能力,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题
| A. | aqn-1 | B. | aqn | C. | $\frac{{a(1-{q^{n-1}})}}{1-q}$ | D. | $\frac{{a(1-{q^n})}}{1-q}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,3] | C. | (1,3) | D. | (1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 8 | C. | 10 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
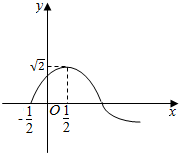 若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )
若函数f(x)=Asin(ωx+φ)(ω>0,A>0,0<φ<π)的部分图象如图所示,则f(0)+f(1)+f(2)+…+f(2008)=( )| A. | 0 | B. | 1 | C. | 2 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{4027}{2}$•32015 | B. | $\frac{3}{2}$+$\frac{4027}{2}$•32015 | C. | 1+$\frac{4027}{2}$•32014 | D. | $\frac{3}{2}$+$\frac{4027}{2}$•32014 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com