
已知以 为首项的数列
为首项的数列 满足:
满足:
(1)若 ,求证:
,求证: ;
;
(2)若 ,求使
,求使 对任意正整数n都成立的
对任意正整数n都成立的 与
与 .
.
科目:高中数学 来源: 题型:解答题
近年来,网上购物已经成为人们消费的一种趋势。假设某淘宝店的一种装饰品每月的销售量y(单位:千件)与销售价格x(单位:元/件)满足关系式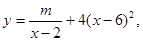 其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
其中2<x<6,m为常数,已知销售价格为4元/件时,每月可售出21千件。(1)求m的值; (2)假设该淘宝店员工工资、办公等每月所有开销折合为每件2元(只考虑销售出的件数),试确定销售价格x的值,使该店每月销售饰品所获得的利润最大.(结果保留一位小数)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某服装厂生产一种服装,每件服装的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100件时,每多订购一件,订购的全部服装的出场单价就降低0.02元,根据市场调查,销售商一次订购量不会超过600件.
(1)设一次订购x件,服装的实际出厂单价为p元,写出函数 的表达式;
的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场销售某种商品的经验表明,该商品每日的销售量 (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式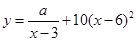 ,其中
,其中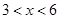 ,
, 为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.已知销售价格为5元/千克时,每日可售出该商品11千克.
(Ⅰ)求 的值;
的值;
(Ⅱ)若该商品的成本为3元/千克,试确定销售价格 的值,使商场每日销售该商品所获得的利润最大.
的值,使商场每日销售该商品所获得的利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我省某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值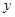 万元与投入
万元与投入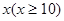 万元之间满足:
万元之间满足: 为常数。当
为常数。当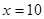 万元时,
万元时,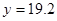 万元;
万元;
当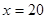 万元时,
万元时,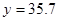 万元。 (参考数据:
万元。 (参考数据: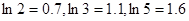 )
)
(1)求 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com