
我省某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值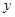 万元与投入
万元与投入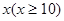 万元之间满足:
万元之间满足: 为常数。当
为常数。当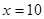 万元时,
万元时,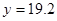 万元;
万元;
当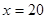 万元时,
万元时,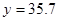 万元。 (参考数据:
万元。 (参考数据: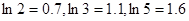 )
)
(1)求 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:高中数学 来源: 题型:解答题
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q亿元),它们与投资额t(亿元)的关系有经验公式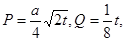 其中
其中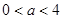 ,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
,今该公司将5亿元投资这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元),
(1)求y关于x的解析式,
(2)怎样投资才能使总利润最大,最大值为多少?.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数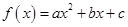 .
.
(1)若对任意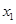 、
、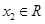 ,且
,且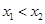 ,都有
,都有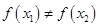 ,求证:关于
,求证:关于 的方程
的方程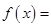
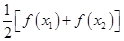 有两个不相等的实数根且必有一个根属于
有两个不相等的实数根且必有一个根属于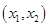 ;
;
(2)若关于 的方程
的方程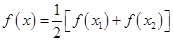 在
在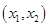 上的根为
上的根为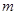 ,且
,且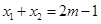 ,设函数
,设函数 的图象的对称轴方程为
的图象的对称轴方程为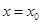 ,求证:
,求证: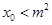 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数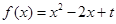 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当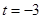 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形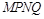 的面积的最大值。
的面积的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数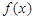 的定义域为
的定义域为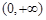 ,若
,若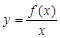 在
在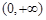 上为增函数,则称
上为增函数,则称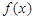 为“一阶比增函数”;若
为“一阶比增函数”;若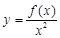 在
在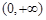 上为增函数,则称
上为增函数,则称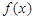 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为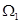 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为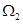 .
.
(Ⅰ)已知函数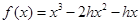 ,若
,若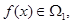 且
且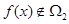 ,求实数
,求实数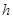 的取值范围;
的取值范围;
(Ⅱ)已知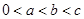 ,
,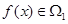 且
且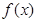 的部分函数值由下表给出,
的部分函数值由下表给出,
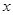 |  | 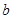 | 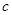 |  |
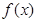 | 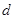 | 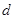 | 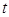 | 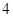 |
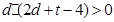 ;
;
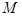 ,使得
,使得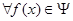 ,
,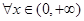 ,有
,有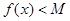 成立?若存在,求出
成立?若存在,求出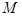 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 .
.
⑴ 求函数 的单调区间;
的单调区间;
⑵ 如果对于任意的 ,
, 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
⑶ 设函数 ,
, . 过点
. 过点 作函数
作函数 图像的所有切线,令各切点的横坐标构成数列
图像的所有切线,令各切点的横坐标构成数列 ,求数列
,求数列 的所有项之和
的所有项之和 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(14分)已知函数 ,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
,其中a是实数.设A(x1,f(x1)),B(x2,f(x2))为该函数图象上的两点,且x1<x2.
(Ⅰ)指出函数f(x)的单调区间;
(Ⅱ)若函数f(x)的图象在点A,B处的切线互相垂直,且x2<0,证明:x2﹣x1≥1;
(Ⅲ)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com