
已知函数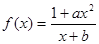
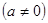 是奇函数,并且函数
是奇函数,并且函数 的图像经过点(1,3).
的图像经过点(1,3).
(1)求实数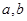 的值;
的值;
(2)求函数 的值域。
的值域。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
我省某景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值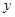 万元与投入
万元与投入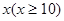 万元之间满足:
万元之间满足: 为常数。当
为常数。当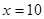 万元时,
万元时,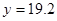 万元;
万元;
当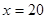 万元时,
万元时,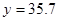 万元。 (参考数据:
万元。 (参考数据: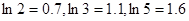 )
)
(1)求 的解析式;
的解析式;
(2)求该景点改造升级后旅游利润 的最大值。(利润=旅游增加值-投入)。
的最大值。(利润=旅游增加值-投入)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产 千件,需另投入成本为
千件,需另投入成本为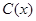 ,当年产量不足80千件时,
,当年产量不足80千件时,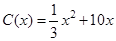 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时,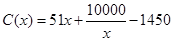 (万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件商品售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(Ⅰ)写出年利润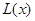 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如果函数f(x)的定义域为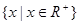 ,且f(x)为增函数,f(xy)=f(x)+f(y)。
,且f(x)为增函数,f(xy)=f(x)+f(y)。
(1)证明: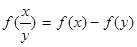 ;
;
(2)已知f(3)=1,且f(a)>f(a-1)+2,求a的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
养路处建造无底的圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12米,高4米。养路处拟另建一个更大的圆锥形仓库,以存放更多食盐。现有两种方案:一是新建的仓库的底面直径比原来增加4米(高不变);二是高度增加4米(底面直径不变)。
分别计算按这两种方案所建的仓库的体积;
分别计算按这两种方案所建的仓库的表面积;
哪个方案更经济些?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知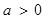 ,函数
,函数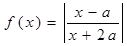 。
。
(I)记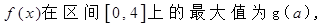 求
求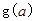 的表达式;
的表达式;
(II)是否存在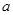 ,使函数
,使函数 在区间
在区间 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com