
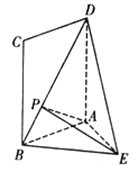
【题目】如图,![]() 为矩形,且平面
为矩形,且平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() .
.
(1)证明:![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用勾股定理可证明![]() ,再由已知的面面垂直得到
,再由已知的面面垂直得到![]() 平面
平面![]() ,从而得到
,从而得到![]() ,进而得到
,进而得到![]() 平面
平面![]() ,最后得到要证明的线线垂直.
,最后得到要证明的线线垂直.
(2)建立如图所示的空间直角坐标系,求出平面![]() 和平面
和平面![]() 的法向量后可求二面角
的法向量后可求二面角![]() 的余弦值.
的余弦值.
(1)证明:由题意知四边形![]() 是矩形,
是矩形,![]() 是以
是以![]() 为直角顶点的等腰直角三角形,且
为直角顶点的等腰直角三角形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,
![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .
.
(2)解:由(1)知![]() ,
,![]() ,
,![]() 两两垂直,
两两垂直,
以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,
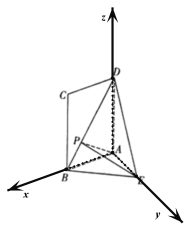
则![]() ,
,
![]() ,
,![]() .
.
设平面![]() 法向量为
法向量为![]() ,则
,则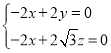 ,
,
取![]() ,则
,则![]() ,
,![]() ,故
,故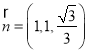 为平面
为平面![]() 的一个法向量,
的一个法向量,
易知平面![]() 的一个法向量为
的一个法向量为![]() .
.
设二面角![]() 的平面角为
的平面角为![]() ,由题中条件可知
,由题中条件可知![]() ,
,
则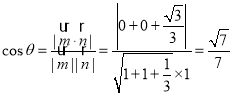 ,
,
![]() 二面角
二面角![]() 的余弦值为
的余弦值为![]() .
.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】某景区提供自行车出租,该景区有辆自行车供游客租赁使用,管理这些自行车的费用是每日![]() 元.根据经验,若每辆自行车的日租金不超过
元.根据经验,若每辆自行车的日租金不超过![]() 元,则自行车可以全部租出;若超出
元,则自行车可以全部租出;若超出![]() 元,则每超过
元,则每超过![]() 元,租不出的自行车就增加
元,租不出的自行车就增加![]() 辆.为了便于结算,每辆自行车的日租金
辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(1)求函数![]() 的解析式;
的解析式;
(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 为
为![]() 平面上一点,有如下三个结论:
平面上一点,有如下三个结论:
①若![]() ,则点
,则点![]() 为
为![]() 的______;
的______;
②若![]() ,则点
,则点![]() 为
为![]() 的______;
的______;
③若![]() ,则点
,则点![]() 为
为![]() 的______.
的______.
回答以下两个小问:
(1)请你从以下四个选项中分别选出一项,填在相应的横线上.
A. 重心 B. 外心 C. 内心 D. 垂心
(2)请你证明结论②.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年9月28日中国女排在世界杯第10轮比赛中,以![]() 的比分战胜塞尔维亚女排,从而在本次女排世界杯中取得10连胜,提前一轮卫冕世界杯冠军.世界杯是单循环赛制,中国女排要和11个对手轮番对决,比赛中以
的比分战胜塞尔维亚女排,从而在本次女排世界杯中取得10连胜,提前一轮卫冕世界杯冠军.世界杯是单循环赛制,中国女排要和11个对手轮番对决,比赛中以![]() 或
或![]() 取胜的球队积3分,负队积0分,而在比赛中以
取胜的球队积3分,负队积0分,而在比赛中以![]() 取胜的球队积2分,负队积1分,通过最终的总积分来决定最后的名次归属.下某网站上整理了2003年以来中国队与世界女排强队的50场比赛胜负情况如下表.
取胜的球队积2分,负队积1分,通过最终的总积分来决定最后的名次归属.下某网站上整理了2003年以来中国队与世界女排强队的50场比赛胜负情况如下表.
中国队和世界女排强队较量的胜负 | |||||||
年份 | 比赛类别 | 古巴 | 巴西 | 俄罗斯 | 意大利 | 美国 | 塞尔维亚 |
2003 | 世界杯 | ○ | ○ | ○ | ○ | ||
2004 | 奥运会(小组赛) | ● | ○ | ○ | |||
2004 | 奥运会(淘汰赛) | ○ | ○ | ||||
2006 | 世锦赛 | ● | ● | ○ | |||
2008 | 奥运会(小组赛) | ● | ● | ||||
2008 | 奥运会(淘汰赛) | ○ | ● | ○ | |||
2010 | 世锦赛 | ○ | ● | ● | |||
2011 | 世界杯 | ● | ● | ● | ○ | ||
2012 | 奥运会 | ● | ● | ○ | |||
2014 | 世锦赛 | ○ | ● | ○ | ● | ○ | |
2015 | 世界杯 | ○ | ○ | ● | |||
2016 | 奥运会(小组赛) | ○ | ○ | ● | ● | ||
2016 | 奥运会(淘汰赛) | ○ | |||||
2018 | 世锦赛(小组赛) | ○ | ● | ○ | |||
2018 | 世锦赛(复赛) | ○ | ● | ○ | |||
2019 | 世界杯 | ○ | ○ | ○ | ○ | ||
说明:○中国队获胜,●中国队败北,比分差:○表示分差为1(例如 | |||||||
(1)若根据表中数据进行推断:求中国队与巴西队比赛获得积分的平均数;
(2)现从中国队与美国比赛获胜的比赛视频中任意调取两场进行观看,求至少有一场是中国队以![]() 获胜的比赛的概率.
获胜的比赛的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在R上的两个周期函数,
是定义在R上的两个周期函数,![]() 的周期为4,
的周期为4,![]() 的周期为2,且
的周期为2,且![]() 是奇函数.当
是奇函数.当![]() 时,
时,![]() ,
, ,其中k>0.若在区间(0,9]上,关于x的方程
,其中k>0.若在区间(0,9]上,关于x的方程![]() 有8个不同的实数根,则k的取值范围是_____.
有8个不同的实数根,则k的取值范围是_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
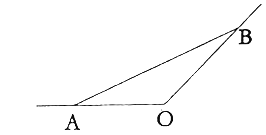
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() 、
、![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“
为“![]() 函数”.
函数”.
(1)试判断函数![]() 与
与![]() 是否是“
是否是“![]() 函数”;
函数”;
(2)若函数![]() 为“
为“![]() 函数”,求实数
函数”,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“
为“![]() 函数”,且
函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com