
【题目】点![]() 为
为![]() 平面上一点,有如下三个结论:
平面上一点,有如下三个结论:
①若![]() ,则点
,则点![]() 为
为![]() 的______;
的______;
②若![]() ,则点
,则点![]() 为
为![]() 的______;
的______;
③若![]() ,则点
,则点![]() 为
为![]() 的______.
的______.
回答以下两个小问:
(1)请你从以下四个选项中分别选出一项,填在相应的横线上.
A. 重心 B. 外心 C. 内心 D. 垂心
(2)请你证明结论②.
【答案】(1)①重心;②内心;③外心. (2)证明见解析.
【解析】
(1)对①,化为![]() 分析即可.
分析即可.
对②,通过运算证明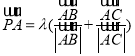 即可证明
即可证明![]() 点在
点在![]() 的角平分线上,同理可证
的角平分线上,同理可证![]() 点在
点在![]() 的角平分线上即可.
的角平分线上即可.
对③,先证明点![]() 为
为![]() 平面上一点,则满足
平面上一点,则满足![]() ,
,![]() 不全为0的点
不全为0的点![]() 是唯一的,再论证当
是唯一的,再论证当![]() 为外心时满足
为外心时满足![]() 即可.
即可.
(1)对①,因为![]() ,故
,故![]() ,取
,取![]() 中点为
中点为![]() ,
,
则![]() ,故
,故![]() 在
在![]() 边的中线
边的中线![]() 上.同理
上.同理![]() 在
在![]() 边的中线上,故
边的中线上,故![]() 为
为![]() 的重心.
的重心.
对②,同解析(2).
对③,先证明点![]() 为
为![]() 平面上一点,则满足
平面上一点,则满足![]() ,
,![]() 不全为0的点
不全为0的点![]() 是唯一的.
是唯一的.
证明:假设还有一点![]() 满足
满足![]() ,则有
,则有![]() ,即
,即
![]() ,故
,故![]() ,此时
,此时![]() 重合.
重合.
所以点![]() 是唯一的.
是唯一的.
再证若![]() 为
为![]() 外心时,
外心时, ![]() .
.
证明:因为![]()
![]()
![]()
所以设![]() 的外接圆半径为
的外接圆半径为![]() 则
则![]()
![]()
![]()
![]()
即![]() .
.
综上所述, ![]() 为
为![]() 外心.
外心.
(2)对![]() ,由正弦定理有
,由正弦定理有![]() .
.
故![]() ,故
,故![]() .
.
即
故 ,故
,故![]() 在
在![]() 的角平分线上,同理可证
的角平分线上,同理可证![]() 点在
点在![]() 的角平分线上.故
的角平分线上.故![]() 为
为![]() 的内心.
的内心.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
【题目】给定函数![]() 和
和![]() ,令
,令![]() ,对以下三个论断:
,对以下三个论断:
(1)若![]() 和
和![]() 都是奇函数,则
都是奇函数,则![]() 也是奇函数;(2)若
也是奇函数;(2)若![]() 和
和![]() 都是非奇非偶函数,则
都是非奇非偶函数,则![]() 也是非奇非偶函数:(3)
也是非奇非偶函数:(3)![]() 和
和![]() 之一与
之一与![]() 有相同的奇偶性;其中正确论断的个数为( )
有相同的奇偶性;其中正确论断的个数为( )
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,全国很多省市将英语考试作为高考改革的重点,一时间“英语考试该如何改革”引起广泛关注,为了解某地区学生和包括老师、家长在内的社会人士对高考英语改革的看法,某媒体在该地区选择了3600人进行调查,就“是否取消英语听力”问题进行了问卷调查统计,结果如下表:
态度 调查人群 | 应该取消 | 应该保留 | 无所谓 |
在校学生 | 2100人 | 120人 |
|
社会人士 | 600人 |
|
|
(1)已知在全体样本中随机抽取![]() 人,抽到持“应该保留”态度的人的概率为
人,抽到持“应该保留”态度的人的概率为![]() ,现用分层抽样的方法在所有参与调查的人中抽取
,现用分层抽样的方法在所有参与调查的人中抽取![]() 人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“应该保留”态度的人中,用分层抽样的方法抽取![]() 人,再平均分成两组进行深入交流,求第一组中在校学生人数
人,再平均分成两组进行深入交流,求第一组中在校学生人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代科学家祖冲之儿子祖暅在实践的基础上提出了体积计算的原理:“幂势既同,则积不容异”(“幂”是截面积,“势”是几何体的高),意思是两个同高的几何体,如在等高处截面的面积恒相等,则它们的体积相等.已知某不规则几何体与如图所示的三视图所表示的几何体满足“幂势既同”,则该不规则几何体的体积为( )
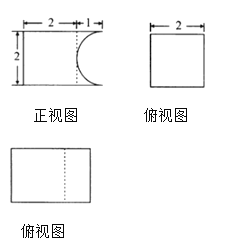
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】曲线![]() 为:到两定点
为:到两定点![]() 、
、![]() 距离乘积为常数
距离乘积为常数![]() 的动点
的动点![]() 的轨迹.以下结论正确的个数为( )
的轨迹.以下结论正确的个数为( )
(1)曲线![]() 一定经过原点;
一定经过原点;
(2)曲线![]() 关于
关于![]() 轴、
轴、![]() 轴对称;
轴对称;
(3)![]() 的面积不大于
的面积不大于![]() ;
;
(4)曲线![]() 在一个面积为
在一个面积为![]() 的矩形范围内.
的矩形范围内.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com