
| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)在区间[0,$\frac{π}{4}$]上是增函数 | |
| C. | 函数f(x)的图象可由g(x)=sin2x的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 函数f(x)的图象关于直线x=$\frac{π}{3}$对称 |
分析 由条件利用正弦函数的周期性、单调性,函数y=Asin(ωx+φ)的图象变换规律,以及函数的图象的对称性,得出结论.
解答 解:对于函数f(x)=sin(2x-$\frac{π}{3}$),它的最小正周期为$\frac{2π}{2}$=π,故A正确;
在区间[0,$\frac{π}{4}$]上,2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{π}{6}$],故函数f(x)在区间[0,$\frac{π}{4}$]上是增函数,故B正确;
把g(x)=sin2x的图象向右平移$\frac{π}{6}$个单位得到函数f(x)=sin(2x-$\frac{π}{3}$)的图象,故C正确;
令x=$\frac{π}{3}$,求得f(x)=$\frac{\sqrt{3}}{2}$,不是函数的最值,故函数f(x)的图象不关于直线x=$\frac{π}{3}$对称,故D不正确,
故选:D.
点评 本题主要考查正弦函数的周期性、单调性,函数y=Asin(ωx+φ)的图象变换规律,以及函数的图象的对称性,属于基础题.


 小学教材全测系列答案
小学教材全测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 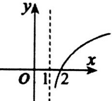 | B. |  | C. | 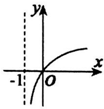 | D. | 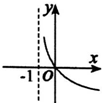 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
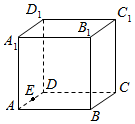 如图,棱长为2的正方体ABCD-A1B1C1D1,E为棱AD的中点,则经过点B1、D1和E三点的截面的左视图的面积为( )
如图,棱长为2的正方体ABCD-A1B1C1D1,E为棱AD的中点,则经过点B1、D1和E三点的截面的左视图的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33人,34人,33人 | B. | 25人,56人,19人 | C. | 30人,40人,30人 | D. | 30人,50人,30人 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com