
分析 (1)由周期函数的定义.
(2)换元,由二次函数的性质得到最值.
(3)由一个周期内的情况类比出2015个零点的情况.
解答 解:(1)函数 f(x)的最小正周期为π.
(2)∵f(x)=a(|sinx|+|cosx|)-sin2x-1,a∈R
=a$\sqrt{1+|sin2x|}$-sin2x-1=a$\sqrt{1+|sin2x|}$-(sin2x+1),
令t=$\sqrt{1+|sin2x|}$,t∈[0,$\sqrt{2}$],
∴y=at-t2=-(t-$\frac{1}{2}$a)2+$\frac{1}{4}$a2,
①$\frac{1}{2}$a≤0时,在t=0处,ymax=0,
②0<$\frac{1}{2}$a<$\sqrt{2}$时,在t=$\frac{1}{2}$a处,ymax=$\frac{1}{4}$a2,
③$\frac{1}{2}$a≥$\sqrt{2}$时,在t=$\sqrt{2}$处,ymax=$\sqrt{2}$a-2.
(3)当a=1时,f(x)=$\sqrt{1+|sin2x|}$-sin2x-1,
∵当且仅当sin2x=0时,f(x)=0,
∴x∈(0,π]时,f(x)有且仅有两个零点分别为$\frac{π}{2}$,π,
∴2015=2×1007+1,
∴k=1008.
点评 本题主要考查周期函数的定义,换元,二次函数的性质以及类比.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
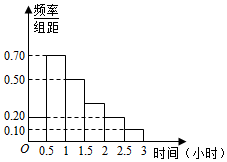 在2016年4月23日“世界读书日”到来之际,某单位对本单位全部200名员工平均每天的读书世界进行了调查,得到如图所示的频率分布直方图,根据该频率分步直方图,估计该单位每天平均读书时间在[1.5,2.5)之间的员工人数为50.
在2016年4月23日“世界读书日”到来之际,某单位对本单位全部200名员工平均每天的读书世界进行了调查,得到如图所示的频率分布直方图,根据该频率分步直方图,估计该单位每天平均读书时间在[1.5,2.5)之间的员工人数为50.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)在区间[0,$\frac{π}{4}$]上是增函数 | |
| C. | 函数f(x)的图象可由g(x)=sin2x的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 函数f(x)的图象关于直线x=$\frac{π}{3}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N | B. | M∪N | C. | ∁R(M∪N) | D. | ∁R(M∩N) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 6 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com