
分析 根据条件容易得到点D为边BC的中点,从而$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,而E为AD上的点,从而有$\overrightarrow{AE}=\frac{k}{2}\overrightarrow{AB}+\frac{k}{2}\overrightarrow{AC}$,且0≤k≤1,而根据$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$便可得到λ=μ,并且$0≤μ≤\frac{1}{2}$,λ=μ带入t=(λ-1)2+μ2并配方便可得出t的最小值.
解答 解:$\overrightarrow{BD}=\overrightarrow{DC}$;
∴D为边BC的中点,如图,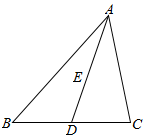
则:$\overrightarrow{AD}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$;
∵E在线段AD上;
∴设$\overrightarrow{AE}=k\overrightarrow{AD}=\frac{k}{2}\overrightarrow{AB}+\frac{k}{2}\overrightarrow{AC}$,0≤k≤1;
又$\overrightarrow{AE}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$;
∴$\left\{\begin{array}{l}{λ=\frac{k}{2}}\\{μ=\frac{k}{2}}\end{array}\right.$;
即λ=μ,且$0≤μ≤\frac{1}{2}$;
∴t=(μ-1)2+μ2
=μ2-2μ+1+μ2
=$2(μ-\frac{1}{2})^{2}+\frac{1}{2}$;
∴$μ=\frac{1}{2}$时,t取最小值$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 考查向量相等的概念,向量加法的平行四边形法则,共线向量基本定理,向量数乘的几何意义,以及平面向量基本定理,配方法求二次函数的最值.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
| 序号 | 分组(分数段) | 频数(人数) | 频率 |
| 1 | [60,70) | 8 | 0.16 |
| 2 | [70,80) | 22 | a |
| 3 | [80,90) | 14 | 0.28 |
| 4 | [90,100) | b | c |
| 合计 | d | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 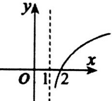 | B. |  | C. | 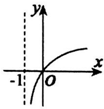 | D. | 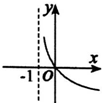 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
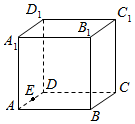 如图,棱长为2的正方体ABCD-A1B1C1D1,E为棱AD的中点,则经过点B1、D1和E三点的截面的左视图的面积为( )
如图,棱长为2的正方体ABCD-A1B1C1D1,E为棱AD的中点,则经过点B1、D1和E三点的截面的左视图的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 33人,34人,33人 | B. | 25人,56人,19人 | C. | 30人,40人,30人 | D. | 30人,50人,30人 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com