
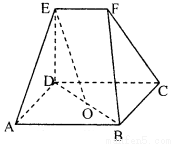
已知矩形ABCD,ED⊥平面ABCD,EF//DC.EF=DE=AD=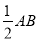 =2,O为BD中点.
=2,O为BD中点.
(Ⅰ)求证:EO//平面BCF;
(Ⅱ)求几何体ABCDEF的体积.
(Ⅰ)详见解析;(Ⅱ)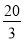 .
.
【解析】
试题分析:(Ⅰ)取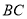 的中点
的中点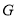 ,连接
,连接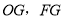 ,可证得:
,可证得: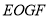 为平行四边形,即
为平行四边形,即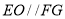 ,进而运用线面平行的判定定理,即可得证;(Ⅱ)将多面体分割成棱锥
,进而运用线面平行的判定定理,即可得证;(Ⅱ)将多面体分割成棱锥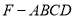 和
和 ,进而运用三棱锥的体积公式即可得到体积.
,进而运用三棱锥的体积公式即可得到体积.
试题解析:证明:(Ⅰ)在矩形ABCD中,取BC的中点G,连接FG,OG

由O为BD中点知,OG∥DC,OG= 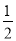 DC,又EF∥DC,EF=
DC,又EF∥DC,EF= 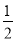 AB=
AB= 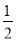 DC
DC
∴OG∥EF且OG=EF,∴OGFE是平行四边形, 4分
∴EO∥FG,又FG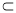 平面BCF,∴EO∥平面BCF 6分
平面BCF,∴EO∥平面BCF 6分
【解析】
(Ⅱ)连接AC,AF,则几何体ABCDEF的
体积为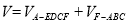 7分
7分
由ED⊥平面ABCD,ABCD为矩形得,AD⊥平面EDCF,
∴AD是四棱锥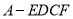 的高,
的高,
又EF∥DC,∴EDCF是直角梯形,又EF=DE=AD=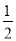 AB=2,
AB=2,
∴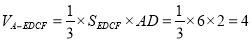 9分
9分
在三棱锥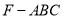 中,高ED=2,
中,高ED=2,
∴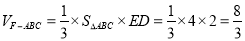 11分
11分
∴几何体ABCDEF的体积为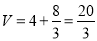 12分.
12分.
考点:1.直线与平面平行的判定;2.棱柱、棱锥、棱台的体积.


科目:高中数学 来源:2015届河南省名校高三上学期期中理科数学试卷(解析版) 题型:解答题
已知数列 的前
的前 项和为
项和为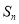 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,
, =
= ,记数列
,记数列 的前
的前 项和
项和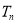 .若对
.若对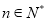 ,
,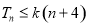 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考理科数学试卷(解析版) 题型:解答题
关于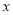 的不等式
的不等式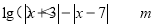 .
.
(Ⅰ)当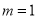 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数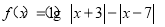 ,当m为何值时,
,当m为何值时,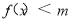 恒成立?
恒成立?
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考理科数学试卷(解析版) 题型:选择题
若[x]表示下超过x的最大整数,执行如图所示的程序框图,则输出的S值为( )
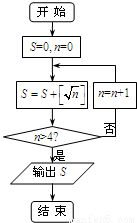
A.4 B.5 C.7 D.9
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:解答题
设函数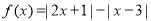 .
.
(Ⅰ)求函数y=f(x)的最小值.
(Ⅱ)若 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届河南省八校高三上学期第一次联考文科数学试卷(解析版) 题型:选择题
某程序框图如右图,当输x=3时,则输出的y=( )
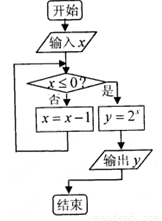
A.1 B.2 C.4 D.8
查看答案和解析>>
科目:高中数学 来源:2015届河南省原名校高三上学期第一次摸底考试数学理科数学试卷(解析版) 题型:填空题
如果双曲线 的渐近线与抛物线
的渐近线与抛物线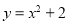 相切,则双曲线的离心率为__________.
相切,则双曲线的离心率为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com