
已知数列{an}的首项a1=a,Sn是数列{an}的前n项和,且满足: =3n2an+
=3n2an+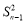 ,an≠0,n≥2,n∈N*.
,an≠0,n≥2,n∈N*.
(1)若数列{an}是等差数列,求a的值;
(2)确定a的取值集合M,使a∈M时,数列{an}是递增数列.
(1)3(2)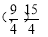
【解析】
试题分析:(1)数列{an}是等差数列,故可从特殊情形出发:先求出a2=12-2a,a3=3+2a.再利用a1+a3=2a2,解得a=3.最后验证.(2)先由通项与和项关系,将已知条件转化为递推关系:an+1+an=6n+3,(n≥2).an+2-an=6,(n≥2),即数列a2,a4,a6, ,及数列a3,a5,a7, 都是公差为6的等差数列,要使数列{an}是递增数列,须有a1<a2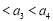 ,解得
,解得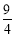 <a<
<a<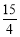 .
.
试题解析:(1)在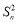 =3n2an+
=3n2an+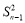 中分别令n=2,n=3,及a1=a得
中分别令n=2,n=3,及a1=a得
(a+a2)2=12a2+a2,(a+a2+a3)2=27a3+(a+a2)2,
因an≠0,所以a2=12-2a,a3=3+2a. 2分
因数列{an}是等差数列,所以a1+a3=2a2,即2(12-2a)=a+3+2a,解得a=3. 4分
经检验a=3时,an=3n,Sn=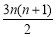 ,Sn-1=
,Sn-1=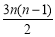 满足
满足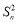 =3n2an+
=3n2an+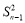
(2)由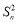 =3n2an+
=3n2an+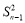 ,得
,得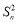 -
-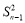 =3n2an,即(Sn+Sn-1)(Sn-Sn-1)=3n2an,
=3n2an,即(Sn+Sn-1)(Sn-Sn-1)=3n2an,
即(Sn+Sn-1)an=3n2an,因为an≠0,所以Sn+Sn-1=3n2,(n≥2),① 6分
所以Sn+1+Sn=3(n+1)2,②
②-①,得an+1+an=6n+3,(n≥2).③ 8分
所以an+2+an+1=6n+9,④
④-③,得an+2-an=6,(n≥2)
即数列a2,a4,a6, ,及数列a3,a5,a7, 都是公差为6的等差数列, 10分
因为a2=12-2a,a3=3+2a.
所以an=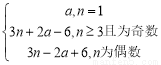 12分
12分
要使数列{an}是递增数列,须有
a1<a2,且当n为大于或等于3的奇数时,an<an+1,且当n为偶数时,an<an+1,
即a<12-2a,
3n+2a-6<3(n+1)-2a+6(n为大于或等于3的奇数),
3n-2a+6<3(n+1)+2a-6(n为偶数),
解得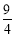 <a<
<a<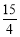 .所以M=
.所以M=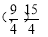 ,当a∈M时,数列{an}是递增数列. 16分
,当a∈M时,数列{an}是递增数列. 16分
考点:等差数列


科目:高中数学 来源:2014-2015学年山东省济南市高三上学期期末考试理科数学试卷(解析版) 题型:选择题
在某项测量中,测量结果X服从正态分布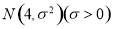 ,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
,若X在(0,8)内取值的概率为0.6,则X在(0,4)内取值的概率为
A.0.2 B.0.3 C.0.4 D.0.6
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省南昌市高三上学期第四次月考理科数学试卷(解析版) 题型:选择题
已知定义在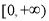 上的函数
上的函数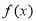 满足
满足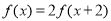 ,当
,当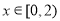 时,
时,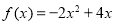 .
.
设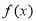 在
在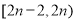 上的最大值为
上的最大值为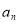 (
(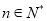 ),且
),且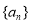 的前
的前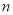 项和为
项和为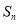 ,则
,则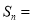 ( )
( )
A.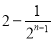 B.
B.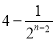 C.
C.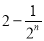 D.
D.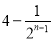
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省南昌市高三上学期第四次月考理科数学试卷(解析版) 题型:选择题
过点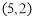 ,且在
,且在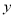 轴上的截距是在
轴上的截距是在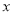 轴上的截距的
轴上的截距的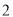 倍的直线方程是( )
倍的直线方程是( )
A.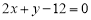 B.
B.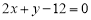 或
或
C.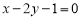 D.
D.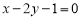 或
或
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三下学期期初开学联考文科数学试卷(解析版) 题型:解答题
(本小题满分14分)
设△ABC三个内角A、B、C所对的边分别为a,b,c. 已知C= ,acosA=bcosB.
,acosA=bcosB.
(1)求角A的大小;
(2)如图,在△ABC的外角∠ACD内取一点P,使得PC=2.过点P分别作直线CA、CD的垂线PM、PN,垂足分别是M、N.设∠PCA=α,求PM+PN的最大值及此时α的取值.


查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三下学期期初开学联考文科数学试卷(解析版) 题型:填空题
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足PD=PF=1,PE=2,则三棱锥P – DEF的体积是 .

查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省宿迁市高三下学期期初开学联考理科数学试卷(解析版) 题型:填空题
如图,点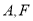 分别是椭圆
分别是椭圆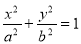
 的上顶点和右焦点,直线
的上顶点和右焦点,直线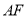 与椭圆交于另一点
与椭圆交于另一点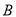 ,过中心
,过中心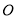 作直线
作直线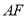 的平行线交椭圆于
的平行线交椭圆于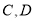 两点,若
两点,若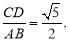 则椭圆的离心率为 .
则椭圆的离心率为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com