
某广场上有4盏装饰灯,晚上每盏灯都随机地闪烁红灯或绿灯,每盏灯出现红灯的概率都是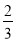 ,出现绿灯的概率都是
,出现绿灯的概率都是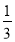 .记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时:
.记这4盏灯中出现红灯的数量为X,当这排装饰灯闪烁一次时:
(1)求X=2时的概率;
(2)求X的数学期望.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.6练习卷(解析版) 题型:解答题
若一批白炽灯共有10000只,其光通量X服从正态分布,其正态分布密度函数是f(x)=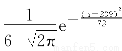 ,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
,x∈(-∞,+∞),试求光通量在下列范围内的灯泡的个数.
(1)(203,215);(2)(191,227).
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:解答题
甲、乙两人各进行3次射击,甲每次击中目标的概率为 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 .
.
(1)求乙至多击中目标2次的概率;
(2)记甲击中目标的次数为Z,求Z的分布列、数学期望和标准差.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:解答题
在高中“自选模块”考试中,某考场的每位同学都选了一道数学题,第一小组选《数学史与不等式选讲》的有1人,选《矩阵变换和坐标系与参数方程》的有5人,第二小组选《数学史与不等式选讲》的有2人,选《矩阵变换和坐标系与参数方程》的有4人,现从第一、第二两小组各任选2人分析得分情况.
(1)求选出的4人均为选《矩阵变换和坐标系与参数方程》的概率;
(2)设X为选出的4个人中选《数学史与不等式选讲》的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.5练习卷(解析版) 题型:填空题
设15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.4练习卷(解析版) 题型:解答题
某大厦的一部电梯从底层出发后只能在第18,19,20层可以停靠,若该电梯在底层载有5位乘客,且每位乘客在这三层的每一层下电梯的概率均为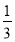 ,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
,用X表示这5位乘客在第20层下电梯的人数,求随机变量X的分布列.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标2.3练习卷(解析版) 题型:填空题
已知A、B是相互独立事件,且P(A)=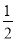 ,P(B)=
,P(B)= ,则P(A
,则P(A )=________;P(
)=________;P(
 )=________.
)=________.
查看答案和解析>>
科目:高中数学 来源:2015届苏教版选修2-3高二数学双基达标1章练习卷(解析版) 题型:填空题
用0,1,2,3,4这五个数字组成无重复数字的五位数,其中恰有一个偶数数字夹在两个奇数数字之间,这样的五位数有________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com