
已知数列{an}和{bn}满足:a1=λ,an+1=![]() 其中λ为实数,n为正整数.
其中λ为实数,n为正整数.
(Ⅰ)对任意实数λ,证明数列{an}不是等比数列;
(Ⅱ)试判断数列{bn}是否为等比数列,并证明你的结论;
(Ⅲ)设0<a<b,Sn为数列{bn}的前n项和.是否存在实数λ,使得对任意正整数n,都有a<Sn<b?若存在,求λ的取值范围;若不存在,说明理由.
(Ⅰ)证明:假设存在一个实数λ,使{an}是等比数列,则有a22=a1a3,即
![]() 矛盾.
矛盾.
所以{an}不是等比数列.
(Ⅱ)解:因为bn+1=(-1)n+1[an+1-3(n-1)+21]=(-1)n+1(![]() an-2n+14)
an-2n+14)
=![]() (-1)n?(an-3n+21)=-
(-1)n?(an-3n+21)=-![]() bn
bn
又b1=-(λ+18),所以
当λ=-18,bn=0(n∈N+),此时{bn}不是等比数列:
当λ≠-18时,b1=-(λ+18) ≠0,由上可知bn≠0,∴![]() (n∈N+).
(n∈N+).
故当λ≠-18时,数列{bn}是以-(λ+18)为首项,-![]() 为公比的等比数列.
为公比的等比数列.
(Ⅲ)由(Ⅱ)知,当λ=-18,bn=0,Sn=0,不满足题目要求.
∴λ≠-18,故知bn= -(λ+18)?(-![]() )n-1,于是可得
)n-1,于是可得
Sn=-![]()
要使a<Sn<b对任意正整数n成立,
即a<-![]() (λ+18)?[1-(-
(λ+18)?[1-(-![]() )n]b(n∈N+)
)n]b(n∈N+)
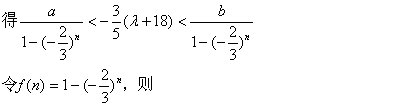 ①
①
当n为正奇数时,1<f(n)![]()
∴f(n)的最大值为f(1)=![]() ,f(n)的最小值为f(2)=
,f(n)的最小值为f(2)= ![]() ,
,
于是,由①式得![]() a<-
a<-![]() (λ+18)<
(λ+18)<![]()
当a<b![]() 3a时,由-b-18
3a时,由-b-18![]() =-3a-18,不存在实数满足题目要求;
=-3a-18,不存在实数满足题目要求;
当b>3a存在实数λ,使得对任意正整数n,都有a<Sn<b,且λ的取值范围是(-b-18,-3a-18).


科目:高中数学 来源: 题型:
| a1an+1 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2n-1 |
| 1 |
| a2n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2n |
| 3 |
| 4 |
| 9 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bn | ||
1-4
|
| 1 |
| an |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com