
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,证明:
时,证明:![]() ;
;
(3)求证:对任意的![]() ,都有:
,都有:![]() ,(其中
,(其中![]() 为自然对数的底数)。
为自然对数的底数)。
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)分别在![]() 和
和![]() 两段范围内讨论导函数的正负,从而得到单调区间;(2)将问题转化为证明
两段范围内讨论导函数的正负,从而得到单调区间;(2)将问题转化为证明![]() ,通过导数求得
,通过导数求得![]() ,从而证得所证不等式;(3)根据(2)可知
,从而证得所证不等式;(3)根据(2)可知![]() ,令
,令![]() ,则可得
,则可得![]() ,再通过
,再通过![]() 进行放缩,证得
进行放缩,证得![]() ,从而得到所证结论.
,从而得到所证结论.
(1)函数![]() 的定义域为
的定义域为![]() ,
,![]()
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
②当![]() 时,令
时,令![]() ,解得:
,解得:![]()
当![]() 时,
时,![]() , 所以
, 所以![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增
上单调递增
综上,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
(2)当![]() 时,
时,![]()
要证明![]() ,即证
,即证![]() ,即
,即![]()
设![]() 则
则![]() ,令
,令![]() 得,
得,![]()
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]()
所以![]() 为极大值点,也为最大值点
为极大值点,也为最大值点
所以![]() ,即
,即![]()
故![]()
(3)由(2)![]() (当且仅当
(当且仅当![]() 时等号成立)
时等号成立)
令![]() , 则
, 则 ![]()
所以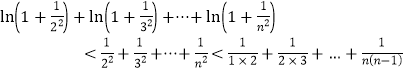
![]()
即![]()
所以![]()


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:
【题目】如图,扇形AOB,圆心角AOB等于60°,半径为2,在弧AB上有一动点P,过P引平行于OB的直线和OA交于点C,设∠AOP=θ,求△POC面积的最大值及此时θ的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】Monte-Carlo方法在解决数学问题中有广泛的应用.下面利用Monte-Carlo方法来估算定积分![]() .考虑到
.考虑到![]() 等于由曲线
等于由曲线![]() ,
,![]() 轴,直线
轴,直线![]() 所围成的区域
所围成的区域![]() 的面积,如图,在
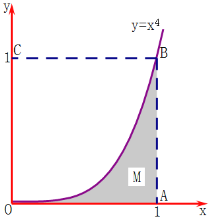
的面积,如图,在![]() 外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为
外作一个边长为1正方形OABC.在正方形OABC内随机投掷n个点,若n个点中有m个点落入M中,则M的面积的估计值为![]() ,此即为定积分
,此即为定积分![]() 的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
的估计值.现向正方形OABC中随机投掷10000个点,以X表示落入M中的点的数目.
(1)求X的期望![]() 和方差
和方差![]() ;
;
(2)求用以上方法估算定积分![]() 时,
时,![]() 的估计值与实际值之差在区间(-0.01,0.01)的概率.
的估计值与实际值之差在区间(-0.01,0.01)的概率.
附表:![]()
| 1899 | 1900 | 1901 | 2099 | 2100 | 2101 |
| 0.0058 | 0.0062 | 0.0067 | 0.9933 | 0.9938 | 0.9942 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.

(I)证明:PQ⊥平面DCQ;
(II)求棱锥Q-ABCD的体积与棱锥P-DCQ的体积的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,过点
,过点![]() 、
、![]() 分别作两平行直线
分别作两平行直线![]() 、
、![]() ,
, ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点, ![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,且当直线
两点,且当直线![]() 过右焦点和上顶点时,四边形
过右焦点和上顶点时,四边形![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若四边形![]() 是菱形,求正数
是菱形,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,其中i为虚数单位,当实数m取何值时,复数z对应的点:
(1)位于虚轴上;
(2)位于一、三象限;
(3)位于以原点为圆心,以4为半径的圆上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】到2020年,我国将全面建立起新的高考制度,新高考采用![]() 模式,其中语文、数学、英语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣、爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门(6选3)参加考试,满分各100分.为了顺利迎接新高考改革,某学校采用分层抽样的方法从高一年级1000名(其中男生550名,女生450名)学生中抽取了
模式,其中语文、数学、英语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣、爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门(6选3)参加考试,满分各100分.为了顺利迎接新高考改革,某学校采用分层抽样的方法从高一年级1000名(其中男生550名,女生450名)学生中抽取了![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中有女生45名,求
名学生中有女生45名,求![]() 的值及抽取的男生的人数.
的值及抽取的男生的人数.
(2)该校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目,且只能选择一个科目),得到如下
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目,且只能选择一个科目),得到如下![]() 列联表.
列联表.
选择“物理” | 选择“地理” | 总计 | |
男生 | 10 | ||
女生 | 25 | ||
总计 |
(i)请将列联表补充完整,并判断是否有![]() 以上的把握认为选择科目与性别有关系.
以上的把握认为选择科目与性别有关系.
(ii)在抽取的选择“地理”的学生中按性别分层抽样抽取6名,再从这6名学生中抽取2名,求这2名中至少有1名男生的概率.
附:![]() ,其中
,其中![]() .
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com