
分析 (1)利用有理数指数幂的性质、运算法则求解.
(2)利用有理数指数幂的性质、运算法则求解.
解答 (本题满分12分)
解:(1)(2a${\;}^{\frac{3}{2}}$b${\;}^{\frac{1}{2}}$)(-6a${\;}^{\frac{1}{2}}$b${\;}^{\frac{1}{3}}$)÷(-3a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$)
=[2×(-6)÷(-3)]${a}^{\frac{3}{2}+\frac{1}{2}-\frac{1}{6}}$${b}^{\frac{1}{2}+\frac{1}{3}-\frac{5}{6}}$
=4${a}^{\frac{11}{6}}$.
(2)($\root{3}{2}$×$\sqrt{3}$)6+($\sqrt{2\sqrt{2}}$)${\;}^{\frac{4}{3}}$-$\root{4}{2}$×80.25-(-2005)0
=$({2}^{\frac{1}{3}}×{3}^{\frac{1}{2}})^{6}$+(${2}^{\frac{1}{2}}×{2}^{\frac{1}{4}}$)${\;}^{\frac{4}{3}}$-${2}^{\frac{1}{4}}×{2}^{\frac{3}{4}-1}$
=22×33+2-7-2-1=100.
点评 本题考查有理数指数幂化简求值,是基础题,解题时要认真审题,注意有理数指数幂的性质、运算法则的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 若直线m、n都平行于平面α,则m∥n | |
| B. | 设α-l-β是直二面角,若直线m⊥l,则m⊥β | |
| C. | 若直线m、n在平面α内的射影依次是一个点和一条直线,且m⊥n,则n在α内或n与α平行 | |
| D. | 设m、n是异面直线,若m与平面α平行,则n与α相交 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\sqrt{2}$ | B. | 1+$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 1+2$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
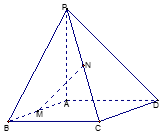 已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点.
已知PA垂直于矩形ABCD所在平面,M,N分别是AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {2,1} | B. | {x=2,y=1} | C. | {(2,1)} | D. | (2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1:1 | B. | 1:2 | C. | 2:1 | D. | 1:3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com