
 53天天练系列答案
53天天练系列答案科目:高中数学 来源:2017届山东枣庄三中高三9月质检数学(文)试卷(解析版) 题型:解答题
已知函数 对于任意
对于任意 ,总有
,总有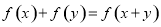 ,且
,且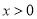 时,
时,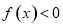 .
.
(1)求证:  在
在 上是减函数;
上是减函数;
(2)若 ,求
,求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源:2017届山东枣庄三中高三9月质检数学(理)试卷(解析版) 题型:填空题
下列四个命题:
① 命题“若 ,则
,则 ” 的否命题是“若
” 的否命题是“若 ,则
,则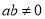 ” ;
” ;
②若命题 ,则
,则 ;
;
③若命题“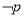 ” 与命题“
” 与命题“ 或
或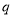 ” 都是真命题, 则命题
” 都是真命题, 则命题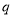 一定是真命题;
一定是真命题;
④命题“若 ,则
,则 ” 是真命题.
” 是真命题.
其中正确命题的序号是 .(把所有正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源:2017届内蒙古高三上入学摸底数学理试卷(解析版) 题型:解答题
某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,并得到如图的频率分布直方图.
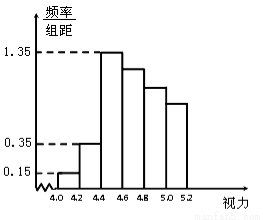
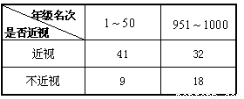
(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数;
(2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到右表中数据,根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(3)在(2)中调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50的学生人数为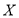 ,求
,求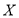 的分布列和数学期望.
的分布列和数学期望.
附:

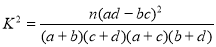
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com