
【题目】已知![]() ,
,![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增;(Ⅱ)
上单调递增;(Ⅱ)![]() .
.
【解析】
(Ⅰ)求函数导数,利用导数可研究函数的单调性;
(Ⅱ)由条件可得![]()
![]() 在
在![]() 上恒成立, 求导得
上恒成立, 求导得![]() ,分别讨论
,分别讨论![]() ,
,![]() 和
和![]() 三种情况,研究
三种情况,研究![]() 的最小值的取值情况,从而即可得解.
的最小值的取值情况,从而即可得解.
(Ⅰ)![]() 时,
时,![]() ,定义域是全体实数,求导得
,定义域是全体实数,求导得![]() ,
,
令![]() ,所以
,所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
(Ⅱ)令![]()
![]() 在
在![]() 上恒成立,则
上恒成立,则![]()
![]() 在
在![]() 上恒成立
上恒成立
求导得![]() .
.
若![]() ,显然
,显然![]() 可以任意小,不符合题意.
可以任意小,不符合题意.
若![]() ,则
,则![]() 最大也只能取0.
最大也只能取0.
当![]() 时,令
时,令![]()
![]() ,
,
于是![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 单调递增,在
单调递增,在![]() 取唯一的极小值也是最小值
取唯一的极小值也是最小值
![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 单调递减,
单调递减,
在![]() 取唯一极大值也是最大值
取唯一极大值也是最大值![]() ,此时
,此时![]() ,
,![]() ,所以
,所以![]() 的最大值等于
的最大值等于![]() .
.
备注一:结合图象,指数函数在直线的上方,斜率![]() 显然,再讨论
显然,再讨论![]() 的情况.
的情况.
备注二:考虑到![]()
![]() 在
在![]() 上恒成立,令
上恒成立,令![]() 即得
即得![]() .取
.取![]() ,
,![]()
证明![]() 在
在![]() 上恒成立也给满分.
上恒成立也给满分.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: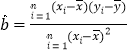 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着人民生活水平的提高,对城市空气质量的关注度也逐步增大,图2是某城市1月至8月的空气质量检测情况,图中一、二、三、四级是空气质量等级, 一级空气质量最好,一级和二级都是质量合格天气,下面四种说法正确的是( )
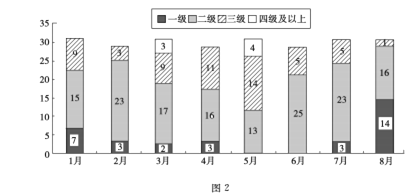
①1月至8月空气合格天数超过20天的月份有5个
②第二季度与第一季度相比,空气达标天数的比重下降了
③8月是空气质量最好的一个月
④6月份的空气质量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,如图,在直二面角![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,且
,且![]() .
.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在线段![]() (不包含端点)上是否存在点
(不包含端点)上是否存在点![]() ,使得
,使得![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;若存在,写出
;若存在,写出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com