练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图, 直线y=x与抛物线y=x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

    (1) 求点Q的坐标；

    (2) 当P为抛物线上位于线段AB下方(含A、B) 的动点时, 求ΔOPQ面积的最大值.

     

    答案：
    解析：

    【解】(1) 解方程组　　  得x1=－4,　　 x2=8  ; y1=－2,    y2=4

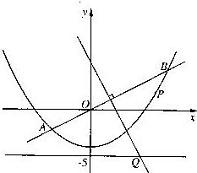
       即A(－4,－2),B(8,4), 从而AB的中点为M(2,1).

       由kAB==,直线AB的垂直平分线方程y－1=(x－2).

       令y=－5, 得x=5, ∴Q(5,－5)

      (2) 直线OQ的方程为x+y=0, 设P(x, x2－4).

       ∵点P到直线OQ的距离d==,

       ,∴SΔOPQ==.

      ∵P为抛物线上位于线段AB下方的点, 且P不在直线OQ上,

      ∴－4≤x<4－4或4－4<x≤8.  ∵函数y=x2+8x－32在区间[－4,8] 上单调递增,

      ∴当x=8时, ΔOPQ的面积取到最大值30.

     

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （04年上海卷文）(本题满分14分) 第1小题满分6分, 第2小题满分8分

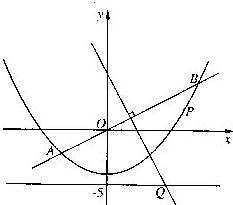
      如图, 直线y=x与抛物线y=x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

     (1) 求点Q的坐标；

    (2) 当P为抛物线上位于线段AB下方

    (含A、B) 的动点时, 求ΔOPQ面积的最大值.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2012年苏教版高中数学选修1-1 2.4抛物线练习卷（解析版） 题型：解答题

    如图, 直线y=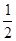x与抛物线y=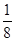x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

    （1）求点Q的坐标；

    （2）当P为抛物线上位于线段AB下方

    （含A、B）的动点时, 求ΔOPQ面积的最大值.

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

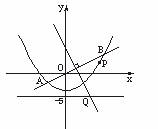    如图, 直线y=x与抛物线y=x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

    （1） 求点Q的坐标；

    （2） 当P为抛物线上位于线段AB下方（含A、B） 的动点时, 求ΔOPQ面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图,直线y=x与抛物线y=x2-4交于A、B两点,线段AB的垂直平分线与直线y=-5交于点Q.

    (1)求点Q的坐标;

    (2)当P为抛物线上位于线段AB下方(含点A、B)的动点时,求△OPQ面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图, 直线y=x与抛物线y=x2－4交于A、B两点, 线段AB的垂直平分线与直线y=－5交于Q点.

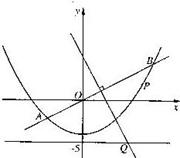     (1) 求点Q的坐标；

    (2) 当P为抛物线上位于线段AB下方

    (含A、B) 的动点时, 求ΔOPQ面积的最大值.

    查看答案和解析>>

    同步练习册答案