
解:(1)定义域为(0,+∞),
由f ′(x)=exlnx(lnx+1),
令f ′(x)>0,解得x>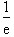 ;令f '(x)<0,解得0<x<
;令f '(x)<0,解得0<x<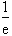 .
.
故f(x)的增区间:(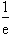 ,+∞),减区间:(0,
,+∞),减区间:(0, ),
),
(2)即证:(x+1)ln(x+1)>2x-1 ln(x+1)>
ln(x+1)>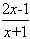
 ln(x+1)-
ln(x+1)-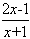 >0
>0
令g(x)=ln(x+1)- ,由g'(x)=
,由g'(x)= ,
,
令g′(x)=0,得x=2,且g(x)在(0,2)↓,在(2,+∞)↑,所以g(x)min=g(2)=ln3﹣1,
故当x>0时,有g(x)≥g(2)=ln3﹣1>0得证。
(3)由(2)得ln(x+1)>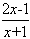 ,即ln(x+1)>2-
,即ln(x+1)>2-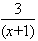 ,
,
所以ln[k(k+1)+1]>2-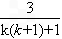 >2-
>2- ,
,
则:ln(1×2+1)+ln(2×3+1)+…+ln[(n(n+1)]+1>(2- )+(2-
)+(2- )+...+[2-
)+...+[2- ]=2n-3+
]=2n-3+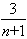 >2n-3。.
>2n-3。.


 53随堂测系列答案
53随堂测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com