练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在四个函数y=sin|x|，y=cos|x|，y= ，y=lg|sinx|中，以π为周期，在 上单调递增的偶函数是（ ）
    A.y=sin|x|
    B.y=cos|x|
    C.y=
    D.y=lg|sinx|

    【答案】D
    【解析】解：由于函数y=sin|x|不具有周期性，故排除A；
    由于函数y=cos|x|在 上单调递减，故排除B；
    由于函数y= 在 上单调递减，故排除C；
    由于函数y=lg|sinx|的周期为π，且是在 上单调递增的偶函数，故满足条件，
    故选：D．
    【考点精析】根据题目的已知条件，利用函数奇偶性的性质的相关知识可以得到问题的答案，需要掌握在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】A. 选修4-1：几何证明选讲

    如图，已知为圆的一条弦，点为弧的中点，过点任作两条弦分别交于点.

    求证：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数 ．
    （1）a的值为多少时，f（x）是偶函数？
    （2）若对任意x∈[0，+∞），都有f（x）＞0，求实数a的取值范围．
    （3）若f（x）在区间[0，+∞）上单调递增，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．　

    （Ⅰ）当时，求函数的极值；

    （Ⅱ）当时，讨论函数单调性；

    （Ⅲ）是否存在实数，对任意的， ，且，有恒成立？若存在，求出的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】质监部门从某超市销售的甲、乙两种食用油中分别各随机抽取100桶检测某项质量指标，由检测结果得到如下的频率分布直方图：

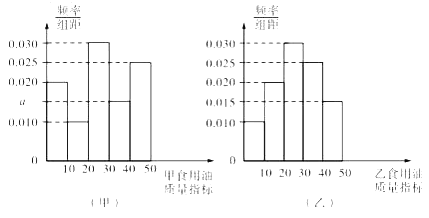
    （Ⅰ）写出频率分布直方图（甲）中的值；记甲、乙两种食用油100桶样本的质量指标的方差分别为，，试比较，的大小（只要求写出答案）；

    （Ⅱ）估计在甲、乙两种食用油中随机抽取1捅，恰有一桶的质量指标大于20；

    （Ⅲ）由频率分布直方图可以认为，乙种食用油的质量指标值服从正态分布．其中近似为样本平均数，近似为样本方差，设表示从乙种食用油中随机抽取10桶，其质量指标值位于（14.55，38.45）的桶数，求的数学期望．

    注：①同一组数据用该区问的中点值作代表，计算得

    ②若，则，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=2sin（2x+ ），g（x）=mcos（2x﹣ ）﹣2m+3（m＞0），若对任意x1∈[0， ]，存在x2∈[0， ]，使得g（x1）=f（x2）成立，则实数m的取值范围是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图几何体中，矩形所在平面与梯形所在平面垂直，且， ， ， 为的中点.

    （1）证明： 平面；

    （2）证明： 平面.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】把下列各命题作为原命题，分别写出它们的逆命题、否命题和逆否命题．

    (1)若α＝β，则sin α＝sin β；

    (2)若对角线相等，则梯形为等腰梯形；

    (3)已知a，b，c，d都是实数，若a＝b，c＝d，则a＋c＝b＋d.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于维向量，若对任意均有或，则称为维向量. 对于两个维向量定义.

    （1）若, 求的值；

    （2）现有一个维向量序列： 若且满足： ，求证：该序列中不存在维向量.

    (3) 现有一个维向量序列： 若且满足： ，若存在正整数使得为维向量序列中的项，求出所有的.

    查看答案和解析>>

    同步练习册答案