
【题目】已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(1)求![]() ,并求
,并求![]() 的单调区间;
的单调区间;
(2)证明:当![]() ,
,![]() 时,
时,![]() .
.
【答案】(1)![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(2)证明见解析.
上单调递减;(2)证明见解析.
【解析】
(1)根据极值点可求出![]() ,根据导函数的正负求出单调区间;
,根据导函数的正负求出单调区间;
(2)法一,由函数单调性可得![]() 变形可得
变形可得![]() ,利用不等式的性质可放缩得到
,利用不等式的性质可放缩得到![]() ,构造函数
,构造函数![]() 可利用导数求最小值为0,即可得证;法二由函数单调性可得
可利用导数求最小值为0,即可得证;法二由函数单调性可得![]() 变形可得
变形可得![]() ,由不等式性质可得
,由不等式性质可得![]() ,令
,令![]() ,由导数可求出
,由导数可求出![]() 即可得证.
即可得证.
(1)![]() ,由
,由![]() 是极值点得
是极值点得![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() 的单调递增区间为
的单调递增区间为![]() ;
;
由![]() 得
得![]() ,∴
,∴![]() 的单调递减区间为
的单调递减区间为![]() .
.
(2)法一:由(1)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() ,即
,即![]() ,故
,故![]() .
.
∴![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
∵![]() ,∴
,∴![]() ,
,
∴![]()
![]() ,
,
∵![]() ,∴
,∴![]() ,∵
,∵![]() ,∴
,∴![]() ,
,
令![]() ,∴
,∴![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,即
,即![]() 在
在![]() 处取等号,
处取等号,
∴![]() ,
,
由于取等条件不同,∴![]() .
.
法二:由(1)可知![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() ,即
,即![]() ,∴
,∴![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
令![]() ,
,![]() ,
,
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递增;
上单调递增;
由![]() 得
得![]() ,∴
,∴![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]() ,
,
由于取等条件不同,故![]() ,整理得
,整理得![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为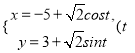 为参数),在以原点
为参数),在以原点![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于
轴分别交于![]() 两点,点
两点,点![]() 是圆
是圆![]() 上任一点,求
上任一点,求![]() 两点的极坐标和
两点的极坐标和![]() 面积的最小值
面积的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全民抗击新冠肺炎疫情期间,北京市开展了“停课不停学”活动,此活动为学生提供了多种网络课程资源以供选择使用.活动开展一个月后,某学校随机抽取了高三年级的甲、乙两个班级进行网络问卷调查,统计学生每天的学习时间,将样本数据分成![]() 五组,并整理得到如下频率分布直方图:
五组,并整理得到如下频率分布直方图:
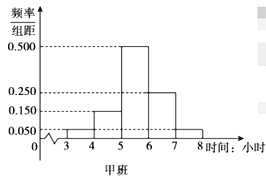
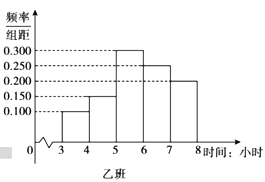
(1)已知该校高三年级共有600名学生,根据甲班的统计数据,估计该校高三年级每天学习时间达到5小时及以上的学生人数;
(2)已知这两个班级各有40名学生,从甲、乙两个班级每天学习时间不足4小时的学生中随机抽取3人,记从甲班抽到的学生人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记甲、乙两个班级学生每天学习时间的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某种同类产品连续十天的销售额(单位:万元),得到如下茎叶图:
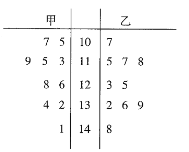
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)如果日销售额超过平均销售额,相应的电商即被评为优,根据统计数据估计两家电商一个月(按30天计算)被评为优的天数各是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递增,下述三个结论:①
单调递增,下述三个结论:①![]() 的取值范围是
的取值范围是![]() ;②
;②![]() 在
在![]() 存在零点;③
存在零点;③![]() 在
在![]() 至多有4个极值点.其中所有正确结论的编号是( )
至多有4个极值点.其中所有正确结论的编号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求 函数![]() 的单调区间;
的单调区间;
(2)定义:对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的不动点. 如果函数
的不动点. 如果函数![]() 存在两个不同的不动点,求实数
存在两个不同的不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
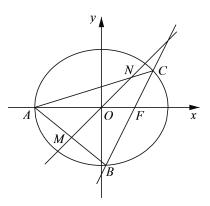
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的右准线为直线
的右准线为直线![]() ,左顶点为
,左顶点为![]() ,右焦点为
,右焦点为![]() . 已知斜率为2的直线
. 已知斜率为2的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 相交于
相交于![]() 两点,且
两点,且![]() 到直线
到直线![]() 的距离为
的距离为![]()
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的直线
的直线![]() 与直线
与直线![]() 分别相交于
分别相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:6月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: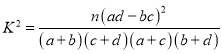 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com