
���� ��1�������⣬��f��x����g��x������h��x�����h��x���ı���ʽ�������ʱh��x�������ֵ���ɣ�
��2���ɶ���д��h��x���ı���ʽ���Լ�L���ܵ�ȡֵ��������þ���ֵ����ʽ���ʼ��ɵõ�����
��3��д��h��x���ĺ�������ʽ������k�IJ�ͬȡֵ���ʱ�����ĵ����ԣ�������Ӧ��Lֵ��
��� �⣺�����⣬��
��1��$h��x��=|{x+\frac{2}{x}-2}|$����x��[1��4]����
$h��x��=x+\frac{2}{x}-2��2\sqrt{2}-2��0$�����ҽ���x=$\frac{2}{x}$��x=$\sqrt{2}$ʱȡ��=����
����$h��x��=x+\frac{2}{x}-2$��
����Ϊh��x����$x��[1\;��\;\sqrt{2}]$ʱ�����ݼ�����$x��[\sqrt{2}\;��\;4]$ʱ����������
��h��1��=1��$h��4��=\frac{5}{2}$��
����h��x����$\frac{5}{2}$��
���Ժ���f��x���ġ�������϶ȡ�$L=\frac{5}{2}$��
��2��h��x��=|f��x��-t|����f��x����[m��n]��
����L��|m-t|��L��|n-t|��
���ԣ�2L��|m-t|+|n-t|��|��m-t��-��n-t��|=|m-n|=n-m��
����2L��n-m����$L��\frac{n-m}{2}$��
��3����Ϊg��x��=kx+t��f��x��=2$\sqrt{x}$��x��[1��4]��
����$h��x��=|2\sqrt{x}-kx-t|$��x��[1��4]��
��$y=2\sqrt{x}-kx$��x��[1��4]��
��k��0ʱ��$y=2\sqrt{x}-kx$��x��[1��4]ʱ����������
����y��[2-k��4-4k]��
�ɣ�2��֪��$L��\frac{4-4k-��2-k��}{2}=\frac{2-3k}{2}$��1��
���Ե�k=0ʱ��ȡ��=����L��СΪ1��
��k��0ʱ��$y=-k{��{\sqrt{x}-\frac{1}{k}}��^2}+\frac{1}{k}$����$\sqrt{x}��[1\;��\;2]$��
�ٵ�$\frac{1}{k}��2$����$0��k��\frac{1}{2}$ʱ��
$y=2\sqrt{x}-kx$��x��[1��4]ʱ����������
����y��[2-k��4-4k]��
�ɣ�2��֪��$L��\frac{4-4k-��2-k��}{2}=\frac{2-3k}{2}$ $��\frac{1}{4}$��
���ҽ���k=$\frac{1}{2}$ʱ��ȡ��=����L��СΪ$\frac{1}{4}$��
�ڵ�$\frac{3}{2}��\frac{1}{k}��2$����$\frac{1}{2}��k��\frac{2}{3}$ʱ��
$y��[{2-k\;��\;\frac{1}{k}}]$��
�ɣ�2��֪��$L��\frac{{k+\frac{1}{k}-2}}{2}��\frac{1}{12}$�����ҽ���$k=\frac{2}{3}$ʱȡ�Ⱥţ�L��СΪ$\frac{1}{12}$��
�۵�$1��\frac{1}{k}��\frac{3}{2}$����$\frac{2}{3}��k��1$ʱ��
$y��[{4-4k\;��\;\frac{1}{k}}]$��
�ɣ�2��֪��$L��\frac{{4k+\frac{1}{k}-4}}{2}��\frac{1}{12}$��
�ܵ�$0��\frac{1}{k}��1$����k��1ʱ��
$y=2\sqrt{x}-kx$��x��[1��4]ʱ�����ݼ���
y��[4-4k��2-k]��
�ɣ�2��֪��$L��\frac{3k-2}{2}��\frac{1}{2}$��
�������������ҽ���$k=\frac{2}{3}$ʱ��${L_{min}}=\frac{1}{12}$��
���� �������ڴ��������ͣ��ؼ����ڶ��¶�������⣬�ڴ˻����Ͽ�����ֵ�����������ֵ����ʽ���Լ��������ۣ�������ѵ�������κ�����صĺ������ۣ�ѧ��ֻҪ���������������ɽ��⣮


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��5�� | B�� | ��6�� | C�� | ��4����5�� | D�� | ��5����6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
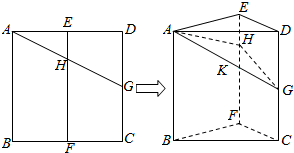
 ��ͼ����֪�ռ��ı���ABCD�У�E��F��G�ֱ���AB��AD��CD�е㣮
��ͼ����֪�ռ��ı���ABCD�У�E��F��G�ֱ���AB��AD��CD�е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | $-\frac{1}{2}$ | C�� | 1 | D�� | 0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | {x|x��-2��0��x��2} | B�� | {x|-2��x��0��x��2} | C�� | {x|-2��x��2} | D�� | {x|-2��x��0��0��x��2} |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com