
分析 利用诱导公式以及辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,结合三角函数的图象和性质,依次判断各选项即可.
解答 解:函数f(x)=cos(2x-$\frac{π}{3}$)+cos(2x+$\frac{π}{6}$)=sin(2x+$\frac{π}{6}$)+cos(2x+$\frac{π}{6}$)=$\sqrt{2}$sin(2x$+\frac{π}{6}+\frac{π}{4}$)=$\sqrt{2}$sin(2x+$\frac{5π}{12}$)
对于①:由三角函数的图象和性质,f(x)的最大值为$\sqrt{2}$;∴①对;
对于②:f(x)最小正周期T=$\frac{2π}{2}=π$,∴②对;
对于③:由$\frac{π}{2}+2kπ≤$2x+$\frac{5π}{12}$$≤\frac{3π}{2}+2kπ$,k∈Z,可得$\frac{π}{24}$+kπ≤x≤$\frac{13π}{24}$+kπ,∴f(x)在区间($\frac{π}{24}$,$\frac{13π}{24}$)上是减函数;∴③对;
对于④:将函数y=$\sqrt{2}$cos2x的图象向右平移$\frac{π}{24}$个单位后,可得$\sqrt{2}$cos2(x-$\frac{π}{24}$)=$\sqrt{2}$cos(2x-$\frac{π}{12}$)=$\sqrt{2}$sin(2x$-\frac{π}{12}$$+\frac{π}{2}$)=$\sqrt{2}$sin(2x+$\frac{5π}{12}$),∴④对.
故答案为:①②③④.
点评 本题主要考查对三角函数的化简能力和三角函数的图象和性质的运用,利用三角函数公式将函数进行化简是解决本题的关键.属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案科目:高中数学 来源: 题型:填空题
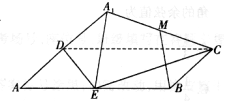 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 使用年数x(单位:米) | 2 | 3 | 4 | 5 | 6 |
| 维修总费用y(单位:万元) | 1.5 | 4.5 | 5.5 | 6.5 | 7.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com