
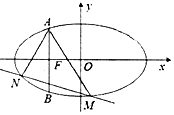
 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.分析 (1)由题意可知c=1,令x=-c,代入椭圆方程可得y=$±\frac{{b}^{2}}{a}$,$\frac{2{b}^{2}}{a}=3,又{a}^{2}={b}^{2}+{c}^{2}$,可得a2=4,b2=3
(2)由(1)知A(-1,$\frac{3}{2}$),设$\overrightarrow{AM},\overrightarrow{AF}的夹角为α$,$\overrightarrow{AN},\overrightarrow{AF}的夹角为β$.由$\frac{{\overrightarrow{AM}•\overrightarrow{AF}}}{{\overrightarrow{|{AM}|}}}=\frac{{\overrightarrow{AN}•\overrightarrow{AF}}}{{\overrightarrow{|{AN}|}}}$得,直线AM、AN的倾斜角互补,直线AM、AN的斜率互为相反数,可设直线AM::y=k(x+1)+$\frac{3}{2}$,代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得$\frac{3}{2}$$(3+4{k}^{2}){x}^{2}+4k(3+2k)x+4{k}^{2}+12k-3=0\\;\\;\$,利用韦达定理求出M、N的坐标,直线MN的斜率kMN=$\frac{{y}_{M}-{y}_{N}}{{x}_{m}-{x}_{N}}=\frac{k({x}_{M}+{x}_{N})+2k}{{x}_{M}-{x}_{N}}=-\frac{1}{2}$.
解答 解:(1)由题意可知F(-1,0),所以c=1,
令x=-c,代入椭圆方程可得y=$±\frac{{b}^{2}}{a}$,∴$\frac{2{b}^{2}}{a}=3,又{a}^{2}={b}^{2}+{c}^{2}$,∴a2=4,b2=3
∴椭圆C的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)由(1)知A(-1,$\frac{3}{2}$),
设$\overrightarrow{AM},\overrightarrow{AF}的夹角为α$,$\overrightarrow{AN},\overrightarrow{AF}的夹角为β$.
由$\frac{{\overrightarrow{AM}•\overrightarrow{AF}}}{{\overrightarrow{|{AM}|}}}=\frac{{\overrightarrow{AN}•\overrightarrow{AF}}}{{\overrightarrow{|{AN}|}}}$得,|$\overrightarrow{AF}$|cosα=|$\overrightarrow{AF}$|cosβ,即∠FAM=∠FAN,又因为FA⊥x轴,
∴直线AM、AN的倾斜角互补,直线AM、AN的斜率互为相反数.
可设直线AM::y=k(x+1)+$\frac{3}{2}$,代入$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$得$\frac{3}{2}$$(3+4{k}^{2}){x}^{2}+4k(3+2k)x+4{k}^{2}+12k-3=0\\;\\;\$,
设M(xM,yM),N(xN,yN),因为A(-1,$\frac{3}{2}$)在椭圆上,
$\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}×(-1)$,${x}_{M}=-\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}$,${y}_{M}=k{x}_{M}+\frac{3}{2}$.
∵直线AM、AN的斜率互为相反数,∴用-k换k得:
${x}_{N}=-\frac{4{k}^{2}-12k-3}{3+4{k}^{2}},{y}_{N}=-kx-k+\frac{3}{2}$.
∴直线MN的斜率kMN=$\frac{{y}_{M}-{y}_{N}}{{x}_{m}-{x}_{N}}=\frac{k({x}_{M}+{x}_{N})+2k}{{x}_{M}-{x}_{N}}=-\frac{1}{2}$.
∴直线MN的斜率是否为定值-$\frac{1}{2}$
点评 本题考查了椭圆与直线的位置关系,定点问题,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损.
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损.| 年龄x(岁) | 20 | 30 | 40 | 50 |
| 周均学习成语知识时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com