
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

分析 (1)从随机数表的第5行第7列的数开始向右读,依次写出抽取的前7人的后三位考号为:310,503,315,571,210,142,188.
(2)这7名同学中数学和物理成绩均为优秀的人数为3人,因此ζ取值为0,1,2,3.ξ~B$(3,\frac{3}{7})$.根据P(ξ=k)=${∁}_{3}^{k}(\frac{4}{7})^{3-k}(\frac{3}{7})^{k}$,即可得出.
解答 解:(1)从随机数表的第5行第7列的数开始向右读,依次写出抽取的前7人的后三位考号为:310,503,315,571,210,142,188.
(2)这7名同学中数学和物理成绩均为优秀的人数为3人,因此ζ取值为0,1,2,3.
ξ~B$(3,\frac{3}{7})$.
∴P(ξ=k)=${∁}_{3}^{k}(\frac{4}{7})^{3-k}(\frac{3}{7})^{k}$,
可得P(ξ=0)=$\frac{64}{343}$,P(ξ=1)=$\frac{144}{343}$,P(ξ=2)=$\frac{108}{343}$,P(ξ=3)=$\frac{27}{343}$.
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{64}{343}$ | $\frac{144}{343}$ | $\frac{108}{343}$ | $\frac{27}{343}$ |
点评 本题考查了二项分布列的概率计算及其数学期望、随机数表的应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | i | B. | -i | C. | -22017i | D. | 22017i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $2\sqrt{3}$ | C. | 4 | D. | $3\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 3.5 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
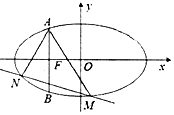 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F为抛物线y2=-4x的焦点,过点F做x轴的垂线交椭圆于A,B两点,且|AB|=3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com