
| A. | π | B. | 3π | C. | 8π | D. | 9π |
分析 过圆锥的旋转轴作轴截面,得△ABC及其内切圆⊙O1和外接圆⊙O2,且两圆同圆心,即△ABC的内心与外心重合,易得△ABC为正三角形,由题意⊙O2的半径为r=2,进而求出圆锥的底面半径和高,代入圆锥体积公式,可得答案.
解答 解:过圆锥的旋转轴作轴截面,得△ABC及其内切圆⊙O1和外接圆⊙O2,
且两圆同圆心,即△ABC的内心与外心重合,易得△ABC为正三角形,
由题意⊙O2的半径为r=2,
∴△ABC的边长为2$\sqrt{3}$,
∴圆锥的底面半径为$\sqrt{3}$,高为3,
∴V=$\frac{1}{3}π×3×3$=3π.
故选B.
点评 本题考查的知识点是旋转体,圆锥的体积,其中根据已知分析出圆锥的底面半径和高,是解答的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
| 数学成绩 | 90 | 97 | 105 | 113 | 127 | 130 | 135 |
| 物理成绩 | 105 | 116 | 120 | 127 | 135 | 130 | 140 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损.
某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各5个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损.| 年龄x(岁) | 20 | 30 | 40 | 50 |
| 周均学习成语知识时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
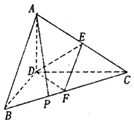 已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.
已知三棱锥A-BCD,AD⊥平面BCD,BD⊥CD,AD=BD=2,CD=2$\sqrt{3}$,E,F分别是AC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com